координаты »
найти координаты - страница 7
1) Е(4;12), F(-4;-10), G(-2;6), H(4;-2)
Найти: а) координаты векторов EF,GH
б) координаты точки О - середины EF
г) уравнение окружности с диаметром FG
д) уравнение прямой FH
2) A(1;1), B(4;2), C(5;5), D(2;4)
Доказать что ABCD - параллелограмм.
Решение: 1) Е(4;12), F(-4;-10), G(-2;6), H(4;-2)
Найти: а) координаты векторов EF,GH
б) координаты точки О - середины EF
г) уравнение окружности с диаметром FG
д) уравнение прямой FH
2) A(1;1), B(4;2), C(5;5), D(2;4)
Доказать что ABCD - параллелограмм.
1) Е(4;12), F(-4;-10), G(-2;6), H(4;-2)
Найти: а) координаты векторов EF,GH
a) ЕF=(-4-4;-10-12)=(-8;-22)
GH=(4-(-2);-2-6)=(6;-8)
б) координаты точки О - середины EF, Е(4;12), F(-4;-10),
О=((4+(-4))/2;(12-10)/2)=(0;1)
г) уравнение окружности с диаметром FG, значит O - центр окружности,
I OF I - радиус
OF=(1/2)EF=(-4;-11) I OF I =√[(-4)²+(-11)²]=√137
уравнение окружности с диаметром FG
(x-0)²+(y-1)²=137
д) уравнение прямой FH
F(-4;-10), H(4;-2)
(x-4)/(4-(-4))= (y-(-2))/(-2-(-10))
(x-4)/(8)= (y+2)/(8)
(x-4)= (y+2)
y=x-6
2) A(1;1), B(4;2), C(5;5), D(2;4)
Доказать что ABCD - параллелограмм.
AB=(4-1;2-1)= (3;1) DC=(5-2;5-4)=(3;1) ⇔ AB=DC(векторы)
BС=(5-4;5-2)=(1;3) AD=(2-1;4-1)=(1;3) ⇔ BC=AD(векторы) ⇔
ABCD - параллелограмм.
Дана система координат Oe1e2, причем |e1|=2, |e2|=корень из 3, угол между ними равен 5pi/6. Найти угол между векторами a(1;2) и b(2;2) и площадь параллелограмма, построенного на векторах a и b.
Решение: Угол между векторами, заданными своими координатами, находится по стандартному алгоритму. Сначала нужно найти скалярное произведение векторов a и b: (a, b) = x1x2 + y1y2 + z1z2. Подставляем сюда координаты данных векторов и считаем:
(a,b) = 8*5 + 10*(-20) = 4*(-10) = 40 - 200 - 40 = -200.
Далее определяем длины каждого из векторов. Длина или модуль вектора - это корень квадратный из суммы квадратов его координат:
|a| = корень из (x1^2 + y1^2 + z1^2) = корень из (8^2 + 10^2 + 4^2) = корень из (64 + 100 + 16) = корень из 180 = 6 корней из 5
|b| = корень из (x2^2 + y2^2 + z2^2) = корень из (5^2 + (-20)^2 + (-10)^2) = корень из (25 + 400 + 100) = корень из 525 = 5 корней из 21.
Перемножаем эти длины. Получаем 30 корней из 105.
И наконец, делим скалярное произведение векторов на произведение длин этих векторов. Получаем,200/(30 корней из 105) или
- (4 корня из 105) / 63. Это - косинус угла между векторами. А сам угол равен арккосинусу из этого числа
ф = arccos(-4 корня из 105) / 63.
Если я всё правильно посчиталДаны
вершины пирамиды А1, А2, А3, А4.
Средствами векторной алгебры найти:
1) длину ребра А1А2;
2) угол между ребрами А1А2 и А1А3;
3) площадь грани А1А2А3 ;
4) объем пирамиды А1А2А3A4
5) длину высоты пирамиды, проведенной
из вершины A4.
Координаты вершин
А1
(1,1,1)
А2 (2,1,1)
А3 (3,1,2)
А4(1,0,3)
Решение: Ох, нелегкая это работа - (из болота тащить бегемота)
за 5 баллов
Смотри решение во вложениях. Должно быть понятно.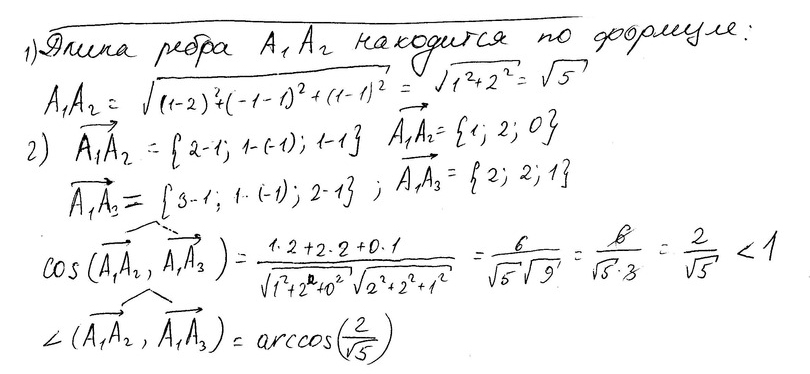
Даны
вершины пирамиды А1, А2, А3, А4.
Средствами векторной алгебры найти:
2) длину ребра А1А2, А1А4;
3) угол между ребрами А1А2 и А1А4;
4) площадь грани А1А2А3 ;
5) объем пирамиды А1А4
Координаты вершин
А1(1;1;-1);
А2(3;2;1);
А3(0;3;0);
А4(3;0;1)
)
Решение: 2) MN = √[(xN-xM)²+(yN-yM)² +(zN-zM)²] ⇒
A1A2=√[(3-1)²+(2-1)²+(1-(-1))²] = √(4+1+4) = 3
A1A4)=√[(3-1)²+(0-1)²+(1-(-1))²]= 3
A1A3=√[(0-1)²+(3-1)²+(0-(-1))²] = √6
A2A3=√[(0-3)²+(3-2)²+(0-1)²] = √11
A2A4=√[(3-3)²+(0-2)²+(1-1)²]= 2
A3A4= √[(3-0)²+(0-3)²+(1-0)²] = √19
3) Вектор → А1А2= →a = (3-1; 2-1; 1-(-1)) = (2;1 ; 2)
→ A1A4= →b =((3-1; 0-1; 1-(-1)) = (2; -1; 2)
cos(a;b)= (a,b)/{IaI·IbI] = [(2·2+1·(-1)+2·2)]/(3·3)= 7/9Даны вершины пирамиды А1, А2, А3, А4.
Средствами векторной алгебры найти:
1) длину ребра А1А2;
2) угол между ребрами А1А2 и А1А3;
3) площадь грани А1А2А3 ;
4) объем пирамиды А1А2А3A4
5) длину высоты пирамиды, проведенной
из вершины A4.
Координаты вершин
А1(2,1,1)
А2 (5,5,4)
А3 (3,2,1)
А4(4,1,3)
Решение: Даны координаты трех точек А1, А2, А3. требуется средствами векторной алгебры найти:
а) длину ВЕКТОРА А1А2
б) скалярное произведение ВЕКТОРОВ А1А2 и А1А3
в) угол между ВЕКТОРАМИ А1А2 и А1А3
г) площадь треугольника А1А2А3
д) уравнение плоскости, проходящей через точки А1, А2, А3
А1(0;2;1) А2(1;-2;1) А3(4;-1;-1)
A1 (x1,y1,z1)
A2 (x2,y2,z2)
A3 (x3,y3,z3)
а) |А1А2| = √( (x2-x1)²+(y2-y1)²+(z2-z1)²)
б) A1A2 * A1A3 = (x2-x1)(x3-x1)+(y2-y1)(y3-y1)+(z2-z1)(z3-z1)
в)
скалярное произведение векторов:
A1A2 * A1A3 = (x2-x1)(x3-x1)+(y2-y1)(y3-y1)+(z2-z1)(z3-z1)
длины векторов:
|А1А2| = √( (x2-x1)²+(y2-y1)²+(z2-z1)²)
|А1А3| = √( (x3-x1)²+(y3-y1)²+(z3-z1)²)
угол между векторами:
cos α = ( ( (x2-x1)(x3-x1)+(y2-y1)(y3-y1)+(z2-z1)(z3-z1) ) / ( √( (x2-x1)²+(y2-y1)²+(z2-z1)²) * √( (x3-x1)²+(y3-y1)²+(z3-z1)²) )
г) площадь треугольника
S= ½ A1A2 * A1A3 = ½((x2-x1)(x3-x1)+(y2-y1)(y3-y1)+(z2-z1)(z3-z1))
д) решение см рисунок
(x-0)((-4)*(-2)-0*(-3))-(y-2)(1*(-2)-0*4) + (z-1)(1*(-3)-(-4)*4) = 0
8(x- 0)+ 2(y - 2)+ 13(z - 1) = 0
8x + 2y + 13z - 17=0

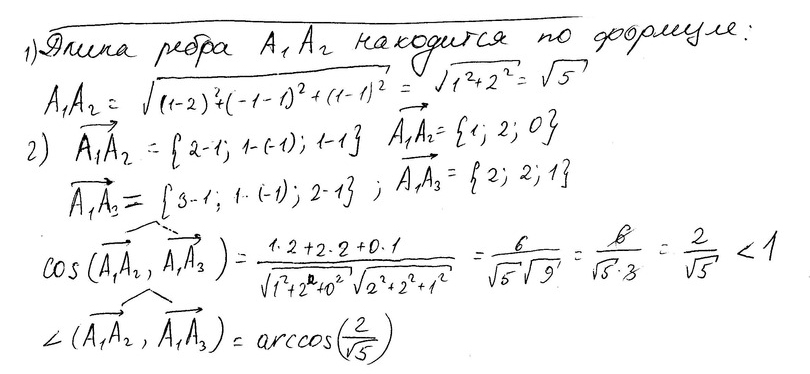
 Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...