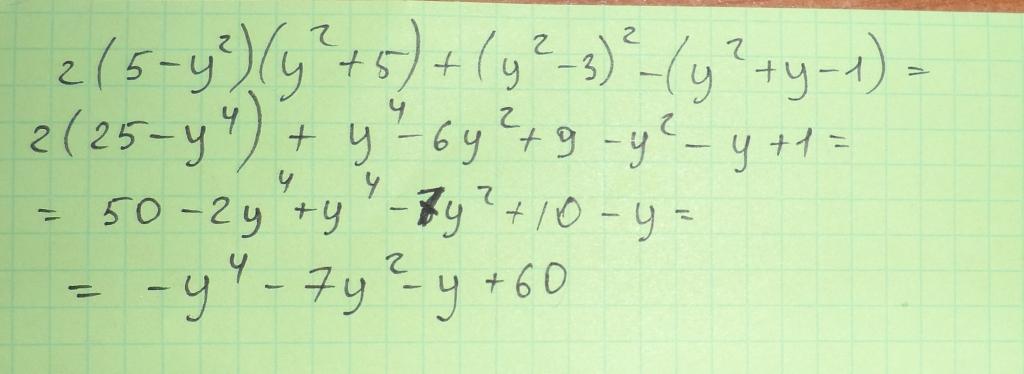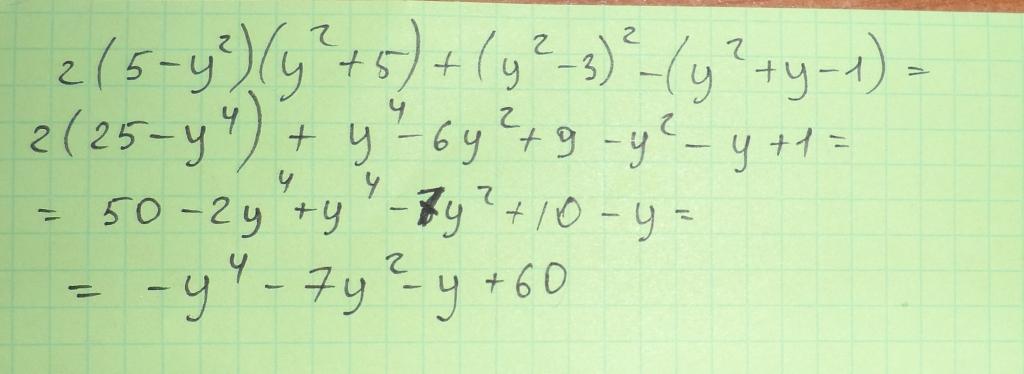преобразуйте выражение в многочлен - страница 11
1. Упростите выражения
а.2x^2×3x^3y^5
Б. (-4ab^3)^2
2. Преобразуйте в многочлен выражение
А. (a+6)^2-2a(3-2a)
Б. (x-2)^2-(x-1)(x+2)
3. решите систему уравнений
A.{2(3x+2y)+9=4x+21
{2x+10=3-(6x+5y)
Б.{2(3x-y)-5=2x-3y
{5-(x-2y)=4y+16
Решение: 1.A.2x²·3x³y⁵=-6x²⁺³y⁵=-6x⁵y⁵=-6(xy)⁵;
Б. (-4ab³)²=16a²b⁶;
2. А.(a+6)²-2a(3-2a)=a²+12a+36-6a+4a²=5a²+6a+36;
Б. (x-2)²-(x-1)(x+2)=x²-4x+4-(x²-x+2x-2)=x²-4x+4-x²-x+2=-5x+6;
3. А.{2(3x+2y)+9=4x+21⇒{6x+4y+9=4x+21 ⇒{2x+4y=12 ⇒2x=12-4y ⇒x=6-2y;
{2x+10=3-(6x+5y) ⇒{2x+10=3-6x-5y ⇒{8x+5y=-7;
8(6-2y)+5y=-7;⇒48-16y+5y=-7;⇒-11y=-55;⇒11y=55;⇒
y=55/11=5;
x=6-2·5=6-10=4;
Б.{2(3x-y)-5=2x-3y ⇒{6x-2y-2x+3y=5;⇒{4x+y=5;⇒y=5-4x;
{5-(x-2y)=4y+16⇒{-x+2y-4y=16-5;⇒{-x-2y=11;
-x-2(5-4x)=11;⇒-x-10+8x=11;⇒7x=21;⇒x=21/7=3;
y=5-4·3=5-12=-7;
Преобразуйте выражение в многочлен: \(2) (0.3a^2+4b)^2\\ 3) (0.2m^2-5n)^2\\ 4) (1.3p^3+2.5p^2)^2 \\ 5) (2.4c^3-1.5d^2)^2 \\ 6) (7x^2y+3xy^2)^2 \)
Решение: $$ 2) (0.3a^2+4b)^2=(0.3a^2+4b)(0.3a^2+4b)= \\ =0.09a^4+1.2a^2b+1.2a^2b+16b^2=0.09a^4+2.4a^2b+16b^2 \\ 3) (0.2m^2-5n)^2=(0.2m^2-5n)(0.2m^2-5n)= \\ =0.04m^4-m^2n-m^2n+25n^2=0.04m^4-2m^2n+25n^2 \\ 4) (1.3p^3+2.5p^2)^2=(1.3p^3+2.5p^2)(1.3p^3+2.5p^2)= \\ =1.69p^6+3.25p^5+3.25p^5+6.25p^4=1.69p^6+6.5p^5+6.25p^4 \\ 5) (2.4c^3-1.5d^2)^2=(2.4c^3-1.5d^2)(2.4c^3-1.5d^2)= \\ =5,76c^6-3,6c^3d^2-3,6c^3d^2+2,25d^4=5,76c^6-7.2c^3d^2+2,25d^4 \\ 6) (7x^2y+3xy^2)^2=(7x^2y+3xy^2)(7x^2y+3xy^2)= \\ =49x^4y^2+21x^3y^3+21x^3y^3+9x^2y^4=49x^4y^2+42x^3y^3+9x^2y^4 $$1. Упростить выражение :
(5х + 4)(25х в квадрате -20х+16)-64
при х = 2.
2. Преобразуйте в многочлен стандартного вида.
(2х+1) в квадрате-(х-5)(х+5)
3. Решить уравнение.
(х-4)(х+4)-6х=(х-2) в квадрате
Решение: $$ 1)(5x+4)(25x^2-20x+16)-64=125x^3-100x^2+80x+ \ \ 100x^2-80x+64-64=125x^3 $$при x=2 $$ 125*2^3=125*8=1000 \\ 2)(2x+1)^2-(x-5)(x+5)=4x^2+4x+1-x^2+25 \\ 3) (x-4)(x+4)-6x=(x-2)^2 $$
$$ x^2-16-6x=x^2-4x+4 $$
$$ x^2-16-6x-x^2+4x-4=0 $$
$$ -2x-20=0 $$
$$ -2x=20 $$
$$ x=-10 $$
1) упростите выражение и найдите его значение:
(5х+4)(25х²-20х+16)-64 при х=2
2) преобразуйте в многочлен стандартного вида:
(2х+1)²-(х-5)(х+5)
Решение: Решениие тоже писать?2) (4X^2+4X+1)-(x^2+5x-5x-25)
4x^2+4x+1-x^2-5x+5x+25
-5x и 5x зачеркиваем и остается
4x^2+4x+1-x^2+25
3x^2+4x+25
Ответ:3x^2+4x+25
1)1)(5x+4)(25x^2-20x+16)-64=125x^3-100x^2+80+100x^2-80x+64-64(64 и -64 зачеркиваем и -100x^2 и 100x^2 тоже зачеркиваем)=125x^3-80x+80
2) Если x=2, то 125x^3-80x+80=125*2^3-80*2+80=1000-160+80=920
Ответ:920
Насчет 1 точно не уверенна)
Преобразуйте алгебраическое выражение в многочлен стандартного вида:
2(5-y в квадрате)(y в квадрате +5)+(y в квадрате - 3) в квадрате -(y в квадрате + y-1)(4-y в квадрате)
Решение: Смотри ответ во вложени$$ 2(5-y) ^{2} (y^2+5)+(y^2-3)^2-(y^2+y-1)(4-y^2)= \\ =2(25-10y+y^2)(y^2+5)+(y^4-6y^2+9)- \\ -(4y^2-y^4+4y-y^3-4+y^2)= \\ =2(25y^2+125-10y^3-50y+y^4+5y^2)+(y^4-6y^2+9)- \\ -(4y^2-y^4+4y-y^3-4+y^2)= \\ =50y^2+250-20y^3-100y+2y^4+10y^2+y^4-6y^2+9- \\ -4y^2+y^4-4y+y^3+4-y^2= \\ =4y^4-19y^3+49y^2-104y+263 $$