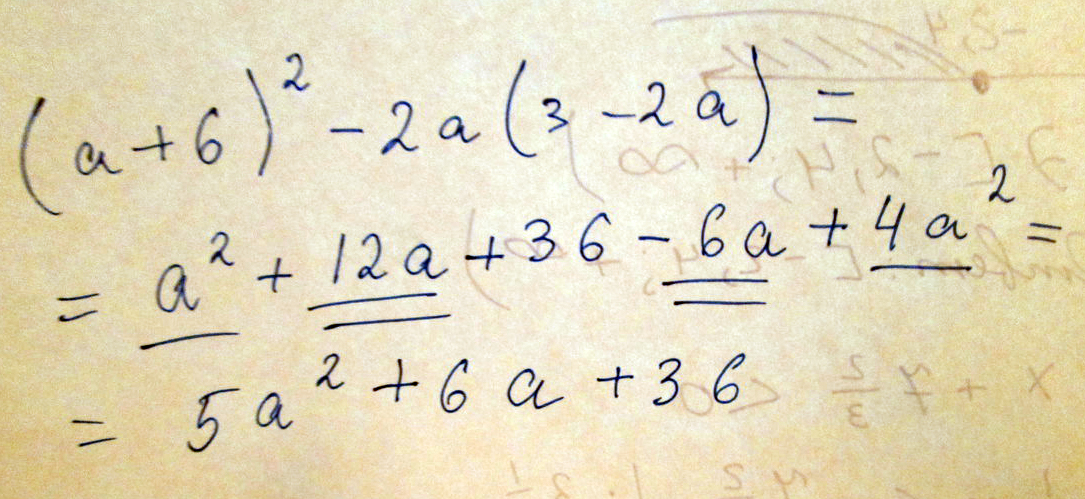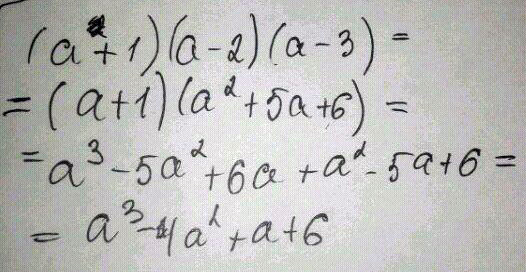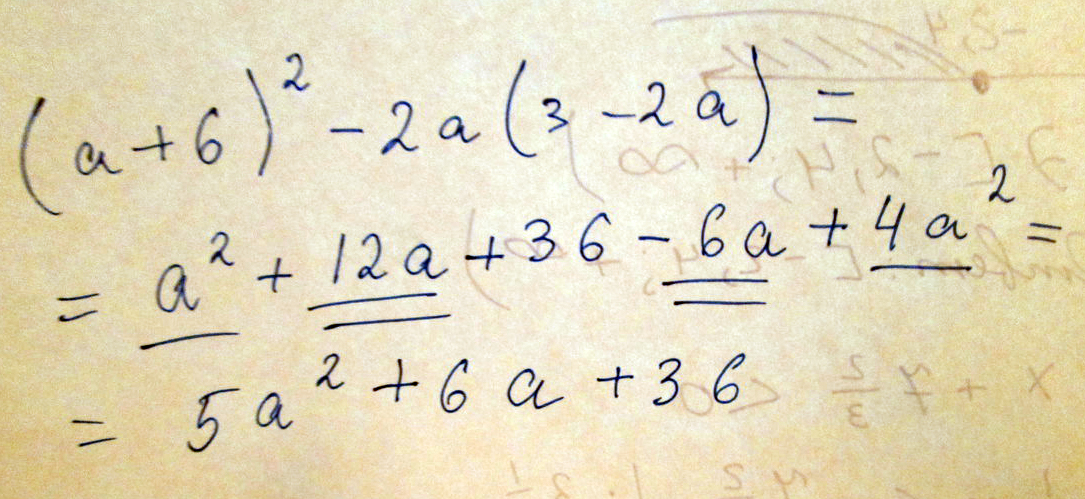многочлен »
преобразуйте выражение в многочлен - страница 9
Преобразуйте в многочлен выражение \((u+2)^3-u(u+4)\)
Решение: Раскроем скобки:
$$ u^3+6u^2+12u+8-u^2-4u=u^3+5u^2+8u+8 $$преобразуйте в многочлен выражение:
(х+6) (х^2-6х+36)-2(х-3)(х+3)
Решение: Х В КУБЕ-2 Х В КВАДРАТЕ+234Решение:
1. x^3+216-2*(x-3)*(x+3)
2. x^3+216-(2*x-6)*(x+3)
3. x^3+216-(2*x^2-18)
4. x^3+216-2*x^2+18
5. x^3+234-2*x^2
Ответ: x^3+234-2*x^2

преобразуйте в многочлен выражение:
1)-(с+5)^2-(c-4)(c+3)
2)(y+2)^2+2(y+1)(y+4)
3)(b-2)b-(b-1)(b+1)
4)2v(v+5)-(v-1)(v^2+v+1)
Решение: Выражение: -(x+5)^2-(x-4)*(x+3)
Ответ: -2*x^2-9*x-13
Решаем по действиям:
1. (x+5)^2=x^2+10*x+25
2.(x^2+10*x+25)=-x^2-10*x-25
3. (x-4)*(x+3)=x^2-x-12
4.x^2-10*x-25-(x^2-x-12)=-x^2-10*x-25-x^2+x+12
5.x^2-x^2=-2*x^2
6.10*x+x=-9*x
7.25+12=-13
Решаем по шагам:
1.(x^2+10*x+25)-(x-4)*(x+3)
2.x^2-10*x-25-(x-4)*(x+3)
3.x^2-10*x-25-(x^2-x-12)
4.x^2-10*x-25-x^2+x+12
5.2*x^2-10*x-25+x+12
6.2*x^2-9*x-25+12
7.2*x^2-9*x-13
Преобразуйте в многочлен выражение (а+1)(а-2)(а-3)
Решение: (a + 1)(a - 2)(a - 3) = (a + 1)(a² - 5a + 6) = a³ - 5a² + 6a + a² - 5a + 6 = a³ - 4a² + a + 6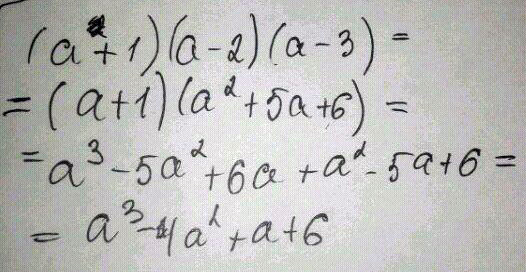
Преобразуйте в многочлен выражение (a+6)^2-2a(3-2a)
Решение: A^2+б^2+2аб-6а+4а^2=5а^2+б^2+2аб-6а