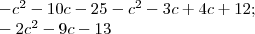преобразуйте выражение в многочлен - страница 8

Преобразуйте в многочлен выражение: 1)-(v - 5)^3 - (v + 2)(v + 3)
2) (x - 4)^2 - 2(x + 1)(x + 4)
3) (a + 3)^3 + (a + 1)(a + 4)

= -(v^3-15v^2+75v-75)-(v^2+3v+2v+6)=-v^3+15v^2-75v+75-v^2-3v-2v-6= -v^3+14v^2-80v+69

2)

= x^2-8x+16-2^x-8x-2x-8=x^2-18x-8

3)

=a^3+9a^2+27a+9+9a^2+4a+a+4=a^3+10a^2+32a+13

1)-(v - 5)^3 - (v + 2)(v + 3) =-(v^3-15v^2+75v-125)-(v^2+3v+2v+6)=- v^3 +15v^2 -75v+125-v^2-3v-2v-6=-v^3+9v^2-75v+125 
2) (x - 4)^2 - 2(x + 1)(x + 4)=x^2-8x+16-2(x^2+4x+x+4)=x^2-8x+16-2x^2-10x-8=-x^2-18x+8
3) (a + 3)^3 + (a + 1)(a + 4)=a^3+9a^2+27a+27+a^2+4a+a+4=a^3+10a^2+32a+31 

Преобразуйте в многочлен выражение:
-(c+5)^2 - (c-4) (c+3)

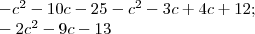
преобразуйте в многочлен выражение \((y+2)^{2} +2y(y+2)\)

Вот так:

$$ 3y^{2}+4y+16 $$

если вы хотели увидеть в конце два выражения в скобках, а между ними умножение, то нужно решить уравнение и записать вот так $$ (X-x_{1})(X-x_{2}) $$

где $$ x_{1}, x_{2} $$ - корни уравнения

а вот так$$ (y + 2)(y-2)+2y^{2}+4y $$ не может быть хотя бы потому что 

$$ (y+2)^{2} = (y+2)(y+2) $$ (с одинаковыми знаками а не с разными)

Преобразуйте в многочлен выражение (a+b)^2*(a-b)^2

Преобразуйте в многочлен выражение: (а-3)(а+1)-(а+6)^3

Ответ: -17*A^2-110*A-219-A^3

Решаем по действиям:
1. (A-3)*(A+1)=A^2-2*A-3
(A-3)*(A+1)=A*A+A*1-3*A-3*1
1.1. A*A=A^2
A*A=A^(1+1)
1.1.1. 1+1=2
+1
_1_
2
1.2. A-3*A=-2*A
2. (A+6)^3=A^3+18*A^2+108*A+216
(A+6)^3=((A+6)*(A+6)*(A+6))
2.1. (A+6)*(A+6)=A^2+12*A+36
(A+6)*(A+6)=A*A+A*6+6*A+6*6
2.1.1. A*A=A^2
A*A=A^(1+1)
2.1.1.1. 1+1=2
+1
_1_
2
2.1.2. A*6+6*A=12*A
2.1.3. 6*6=36
X6
_6_
36
2.2. (A^2+12*A+36)*(A+6)=A^3+18*A^2+108*A+216
(A^2+12*A+36)*(A+6)=A^2*A+A^2*6+12*A*A+12*A*6+36*A+36*6
2.2.1. A^2*A=A^3
A^2*A=A^(2+1)
2.2.1.1. 2+1=3
+2
_1_
3
2.2.2. A*A=A^2
A*A=A^(1+1)
2.2.2.1. 1+1=2
+1
_1_
2
2.2.3. A^2*6+12*A^2=18*A^2
2.2.4. 12*6=72
X12
_ _6_
72
2.2.5. 72*A+36*A=108*A
2.2.6. 36*6=216
X36
_ _6_
216
3. A^2-2*A-3-(A^3+18*A^2+108*A+216)=A^2-2*A-3-A^3-18*A^2-108*A-216
4. A^2-18*A^2=-17*A^2
5.2*A-108*A=-110*A
6.3-216=-219
+216
_ _ _3_
219

Решаем по шагам:
1. A^2-2*A-3-(A+6)^3
1.1. (A-3)*(A+1)=A^2-2*A-3
(A-3)*(A+1)=A*A+A*1-3*A-3*1
1.1.1. A*A=A^2
A*A=A^(1+1)
1.1.1.1. 1+1=2
+1
_1_
2
1.1.2. A-3*A=-2*A
2. A^2-2*A-3-(A^3+18*A^2+108*A+216)
2.1. (A+6)^3=A^3+18*A^2+108*A+216
(A+6)^3=((A+6)*(A+6)*(A+6))
2.1.1. (A+6)*(A+6)=A^2+12*A+36
(A+6)*(A+6)=A*A+A*6+6*A+6*6
2.1.1.1. A*A=A^2
A*A=A^(1+1)
2.1.1.1.1. 1+1=2
+1
_1_
2
2.1.1.2. A*6+6*A=12*A
2.1.1.3. 6*6=36
X6
_6_
36
2.1.2. (A^2+12*A+36)*(A+6)=A^3+18*A^2+108*A+216
(A^2+12*A+36)*(A+6)=A^2*A+A^2*6+12*A*A+12*A*6+36*A+36*6
2.1.2.1. A^2*A=A^3
A^2*A=A^(2+1)
2.1.2.1.1. 2+1=3
+2
_1_
3
2.1.2.2. A*A=A^2
A*A=A^(1+1)
2.1.2.2.1. 1+1=2
+1
_1_
2
2.1.2.3. A^2*6+12*A^2=18*A^2
2.1.2.4. 12*6=72
X12
_ _6_
72
2.1.2.5. 72*A+36*A=108*A
2.1.2.6. 36*6=216
X36
_ _6_
216
3. A^2-2*A-3-A^3-18*A^2-108*A-216
3.1. A^2-2*A-3-(A^3+18*A^2+108*A+216)=A^2-2*A-3-A^3-18*A^2-108*A-216
4.17*A^2-2*A-3-A^3-108*A-216
4.1. A^2-18*A^2=-17*A^2
5.17*A^2-110*A-3-A^3-216
5.1.2*A-108*A=-110*A
6.17*A^2-110*A-219-A^3
6.1.3-216=-219
+216
_ _ _3_
219

раскрываем скобки а^2-2a-3-a^3+18a^2+216a+216=-a^3-17a^2-218a-219