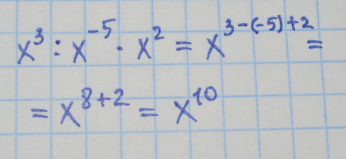преобразуйте выражение в многочлен - страница 5

2. Представьте в виде степени выражение
1)x⁸· x² 1)(x⁸)²
2)x⁸: x² 4)(x⁴)⁵· x²
__________x¹²
4. Представьте в виде многочлена стандартного вида выражение (5x²+6x-3)-(2x²-3x-4)
5. вычислите
1)4⁶·2⁹ 2) (2 2)⁵ · (3)⁶
_32⁴_____3___8
3. Преобразуйте выражения в одночлен стандартного вида. 1)-3a²b⁴· 3a²· b⁵ 2)(-4a²b⁶)³
6. упростите выражение. 125a⁶b³·(-0,2a²b⁴)³

1) Преобразуйте выражение (2х-1)^2-4(x+1) в многочлен стандартного вида
2) Представьте уравнение х^3/x^-5 * x^2 в виде степени к основанием х
3) Решите уравнение 4(х-2)=х+7

1) (2х-1)²-4(x+1)=4х²-4х+1-4х-4=4х²-8х-3
2) х³/x⁻⁵ * x²=х³⁺⁵ * х²=х⁸ * х²=х⁸⁺²=х¹⁰
3)4(х-2)=х+7
4х-8=х+7
4х-х=7+8
3х=15
х=15/3=5
отв:5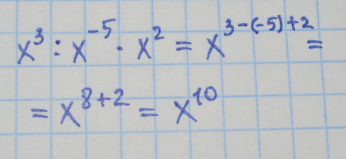

1) преобразуйте в многочлен выражение:
2*(b+1)*(b+4)+(b-6)*(b^2+6b+36)
2) разложить трехчлен на множители:
C^10-2n^4*c^5+n^8
3) разложить трехчлен на множители:
100-20a^4+a^8
4) разложить на множители :
49p^2-64a^2
5) преобразуйте в многочлен выражение:
-(y-1)*y-(y-3)(y+3)
6) разложить на множители:
144-(2p+3)^2
7) решите уравнение:
-x^2-36=0
8) преобразуйте в многочлен выражение:
-x(x+2)-(x-7)(x^2+7x+49)
9) представить квадрат двучлена в виде многочлена:
(13-12n^5)^2
10) разложите на множители:
16-(n+5)^2

1. Представьте в виде многочлена: а) (x-2y) в квадрате; б) (1,4m-n) (1,4m+n)
2. Преобразуйте в произведение: а) 36а в квадрате -b в квадрате; б) 4-4с+с в квадрате; в) 15y в кубе - 3y в кубе
3. Вычислите, не используя калькулятор и таблицы (25,9 в квадрате - 4,1 в квадрате):15
4. Упростите выражение (c-d) d в квадрате +d(5c-d) и найдите его значение при с=-2, d=1,3
5. Решите уравнение: 49-(x+5) в квадрате=0

(х-2у)^2=х^2-4ху+4у^2
(1.4м-н)(1.4м+н)=1.96м^2-н^2
36а^2-б^2=(6а-б)(6а+б)
4-4с+с^2=4-2с-2с+с^2=(4-2с)-(2с-с^2)=
=2(2-с)-с(2-с)=(2-с)(2-с)=(2-с)^2
15у^3-3у^3=12у^3
49-(х+5)^2=0
49-х^2-10х-25=0
-х^2-10х+24=0
х^2+10х-24=0
Д=100-4×1×(-24)=196
х1=(-10-14)/2=-12
х2=(-10+14)/2=2

1. Преобразуйте выражение в многочлен.
а) (2m+3n)²=
б) (0,6-y)²=
в) (a²:5-15b)²
г ) (-2-n)²=
2. упростите выражение и найдите его значение :
а) (y-2)²+y(y+4) при y=-0,5
б) 4p(p-5)-(2p-3)² при p= 1,25
3. используя формулу квадрата суммы или разности, вычислите :
а) 51²=(50+1)²=
б) 28²=
4. Представьте произведение в виде многочлена:
а) (a-8)(a+8)=
б) (x²+4)(x²-4)=
в) (0,2m+10n)(0,2m-10n)=
г) (3b²+5a)(5a-3b²)
5. Воспользуйтесь формулой "Разность квадратов" для вычисления произведения:
a) 53*47=(50+3)(50-3)=
б) 62*58
6. Упростите выражение:
(b-2a)²-(2b+a)(2b-a)=

1) a) =4m²+12mn+9n²
b) =0.36 - 1.2y + y²
в) =a^4/25 -2*a²/5*15b +225b² =a^4/25 - 6a²b +225b²
г) (-2-n)² =(-2)²-2*(-2)*n +n²
=4 +4n +n²
значок ^ обозначает в степени
2. a) (y-2)²+y(y+4)=
=y²-4y+4+y²+4y=2y²+4=
=2(y²+2)= -0.5(-0.5)²+2)= -1.125 4p²-20p-4p²+12p-9=
= -8p-9= -8*1.25 -9*1.25=
= -10-11.25= -21.25
3. a) 51²=(50+1)²=50²+ 2*50*1+1²=2500+100+1=
=2601
b) 28²=(29-1)²=29²-2*29*1+1²=
=841 -58 +1=784
4. a) (a-8)(a+8)=a²-64
b) (x²+4)(x²-4)=x^4-16
в) 0.2²m²-10²n²=
=0.04m² - 100n²
г) =25a² -9b^4
5. a) 53*47=(50+3)(50-3)=
=50²-9=2500-9 = 2 491
b) 62*58=(60+2)(60-2)=
=60²-4=3600-4 = 3 596
6. (b-2a)² -(2b+a)(2b-a) =
=(b-2a)² -(4b²-a²) =
=b²-4ab+4a²-4b²+a²=
=5a² -4ab -3b²