интеграл »
вычислить интеграл - страница 6
Вычислить интеграл:
\( \int\limits { \frac{x+2}{x^3-2x^2+2x} } \, dx \)
Решение: Разложим подинтегральную дробь на простейшие дроби.
Для этого разложим знаменатель на множители
х³-2х²+2х=х(х²-2х+2)
Дискриминант квадратного трехчлена х²-2х+2 отрицательный, поэтому на множители не раскладывается
$$ \frac{x+2}{x(x^2-2x+2)} = \frac{A}{x} + \frac{Mx+N}{x^2-2x+2} $$
Приводим к общему знаменателю правую часть и приравниваем только числители
х+2=А·(х²-2х+2)+Mx²+Nx
х+2=(А+M)x²+(N-2A)x+2A
Слева многочлен первой степени, но его можно записать и как многочлен второй степени, если приписать 0·х²
Приравниваем коэффициенты при одинаковых степенях х слева и справа
A+M=0
N-2A=1
2A=2
A=1
M=-1
N=1+2A=1+2=3
$$ 1)\int \frac{dx}{x}=ln|x|+C_1 \\ 2)\int \frac{(-x+3)}{x^2-2x+2} dx= \int \frac{(-x+3)}{(x^2-2x+1)+1} dx= \int \frac{(-x+3)}{(x-1)^2+1} dx= $$
Замена переменной
(х-1)=t
x=t+1
dx=dt
$$ =\int \frac{(-(t+1)+3)}{t^2+1} dt=\int \frac{2-t}{t^2+1} dt=\int \frac{2}{t^2+1} dt-\int \frac{t}{t^2+1} dt= \\ \\ =2arctgt- \frac{1}{2}ln|t^2+1 |+C_2= 2arctg|x-1|- \frac{1}{2}ln|x^2-2x+2 |+C_2 $$
Ответ.
$$ ln|x|+C_1+2arctg|x-1|- \frac{1}{2}ln|x^2-2x+2 |+C_2= \\ \\ =ln|x|+2arctg|x-1|- \frac{1}{2}ln|x^2-2x+2 |+C $$
№1 Вычислить интеграл
\( \int\limits^1_2 {(3-4x)} \, dx \) (двойка с минусом -2)
\( \int\limits^ \pi _0 {(sin \frac{x}{3} )} \, dx \)
№2
y=(x+1)^2 +1
y=2
Скрин к №2
Решение: 1
$$ =3x-2 x^{2} =(3-2)-(-6+8)=-1 $$
2
$$ =-3cos \frac{x}{3} =-3cos \frac{ \pi }{3}+3cos0= - \frac{3}{2} +3=1,5 $$
3 Найдем точки пересечения этих графиков
$$ x^{2} +2x+1+1=2 \\ x^{2} +2x=0 \\ x_{1}=0 \\ x_{2}=-2 \\ \int\limits^0_{-2} ({2- x^{2} -2x-2)} \, dx = -\int\limits^0_{-2} { (x^{2} +2x)} \, dx =-( \frac{ x^{3} }{3} + x^{2} )=0+ \frac{8}{3} +4= \ 6 \frac{2}{3} $$
Вычислить интеграл, пользуясь формулой Ньютона-Лейбница
\( \int\limits^3_2 {5xdx/(x-1)( x^{2} +2x+2)} \, \)
Решение: $$ \int \frac{5x\cdot dx}{(x-1)(x^2+2x+2)} =I\\\\ \frac{5x}{(x-1)(x^2+2x+2)} = \frac{A}{x-1} + \frac{Bx+C}{x^2+x+2} =\\= \frac{(A+B)x^2+(2A-B+C)x+(2A-C)}{(x-1)(x^2+2x+2)} \\\\x^2\; |\; A+B=0\;,\qquad \quad A=-B\\\\x^1\; |\; 2A-B+C=5\;,\qquad -3B+C=5\;,\; -3B-2B=5,\; B=-1\\\\x^0\; |\; 2A-C=0\;,\qquad\quad C=2A=-2B\\\\B=-1,\; A=1,\; C=2. \\ I=\int \frac{dx}{x-1} +\int \frac{-x+2}{x^2+2x+2} dx=ln|x-1|-\int \frac{x-2}{(x+1)^2+1} dx=\\\\=[\, x+1=t\;,\; x=t-1\;,\; dx=dt\, ]=\\\\=ln|x-1|-\int \frac{t-3}{t^2+1} dt=ln|x-1|-\int \frac{t\, dt}{t^2+1} +3\int \frac{dt}{t^2+1} = \\ =[u=t^2+1,du=2t*dt]= \\ =ln|x-1|-\frac{1}{2}\int \frac{du}{u}+3arctgt=\\\\=ln|x-1|-\frac{1}{2}ln|u|+3arctg(x+1)+C=\\\\=ln|x-1|-\frac{1}{2}ln|x^2+2x+2|+3arctg(x+1)+C $$Вычислить интеграл рационально :\( \int{(\frac{1+sin^2x}{sin^2x}+3*sin\frac{x}{2}-\frac{1}{x\sqrt{x}})}\, dx \)
Решение: Сначала упростим подынтегральное выражение.$$ \frac{1+sin^2x}{sin^2x} $$
Разделим каждое слагаемое из числителя на знаменатель, получим
$$ \frac{1}{sin^2x}+1 $$
Теперь упростим
$$ \frac{1}{x\sqrt{x}}=x^{-3/2} $$
Теперь будем вычислять интеграл. Т. к. нет пределов, то просто найду первообразную
$$ \int{(\frac{1}{sin^2x}+1+3sin\frac{x}{2}-x^{-\frac{3}{2}}})\, dx=-ctgx+x-6cos\frac{x}{2}+2x^{-\frac{1}{2}} $$
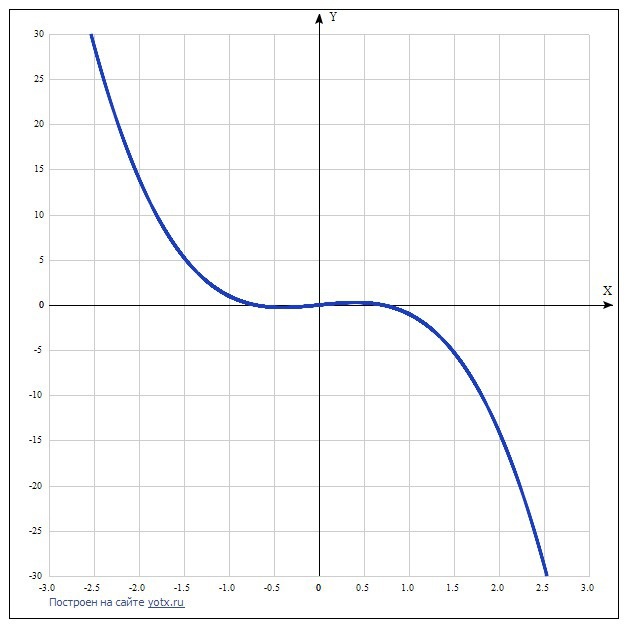
1) Исследовать функцию и построить график:
y=x-2x^3
2) Решить систему уравнений:
x+y-3z= -1
2x-3y+z=0
4x+3y-2z=5
3) вычислить интеграл:
(5x^2-9)dx
Решение: 1) f(x)=−2x³+xТочки пересечения с осью координат YГрафик пересекает ось Y, когда x равняется 0:
подставляем x = 0 в x - 2*x^3.
Результат:
f(0)=0Точка:
(0, 0)
График пересекает ось X, когда y равняется 0:
подставляем 0 = x - 2x³ = x(1 - 2x²).
Отсюда имеем 3 точки пересечения с осью Ох:
х = 0, х = 1/√2 и х = -1/√2.
f = -2*x^3 + xДля того, чтобы найти экстремумы, нужно решить уравнениеf’(x)=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:f’(x)= −6x²+1=0Решаем это уравнение
Корни этого уравнения
x1=−1/√6x2=1/√6
Значит, экстремумы в точках: (-0.40825;-0.27217)
(0.408248; 0.27217).
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
х = -0.5 -0.40825 -0.3 0.3 0.408248 0.5
y’ =-6x^2+1 -0.5 0 0.46 0.46 0 -0.5.
Где производная меняет знак с - на + это минимум, а где с + на - это максимум.
Минимум функции в точке:
x1=−1/√6.
Максимум функции в точке:
x2=1/√6.
Убывает на промежутках [-sqrt(6)/6, sqrt(6)/6]
Возрастает на промежутках
(-oo,sqrt(6)/6] U [sqrt(6)/6, oo) Найдем точки перегибов, для этого надо решить уравнение
f’’(x)=0(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции,
f’’(x)=−12x=0. Решаем это уравнение
Корни этого уравнения
x1=0Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
(-oo, 0]
Выпуклая на промежутках
[0, oo) Горизонтальные асимптотыГоризонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
limx→−∞(−2x3+x)=∞limx→−∞(−2x3+x)=∞
значит,
горизонтальной асимптоты слева не существует
limx→∞(−2x3+x)=−∞limx→∞(−2x3+x)=−∞
значит, горизонтальной асимптоты справа не существуетНаклонную асимптоту можно найти, подсчитав предел функции x - 2*x^3, делённой на x при x->+oo и x->-oo
limx→−∞(1x(−2x3+x))=−∞limx→−∞(1x(−2x3+x))=−∞
значит, наклонной асимптоты слева не существует
limx→∞(1x(−2x3+x))=−∞limx→∞(1x(−2x3+x))=−∞
значит, наклонной асимптоты справа не существуетЧётность и нечётность функции
Проверим функцию чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
x - 2*x³ = -x + 2*x³
- Нет
x - 2*x³ = -x - 2*x³
- Нет, значит, функция не является ни чётной, ни нечётной.
2) Решить систему уравнений:
x+y-3z= -1 2x+2y-6z= -2 2x-3y+z=0 4x+4y-12z=-4
2x-3y+z=0 -2x+3y-z=0 4x+3y-2z=5 -4x-3y+ 2z =-5
4x+3y-2z=5 -
5у -7z = -2 6x - z =5 y -10z =-9
5у -7z = -2 5у -7z = -2 6x=z+5 y = 10z -9
y -10z =-9 -5y+50z = 45 x=(1+5)/6 = 1. y= 10*1-9=1.
-
43z = 43
z = 1.
Ответ: x = 1, y = 1, z = 1.
3) вычислить интеграл (5x^2-9)dx.
$$ \int\limits {(5x^2-9)} \, dx = \frac{5x^3}{3} -9x+C. $$