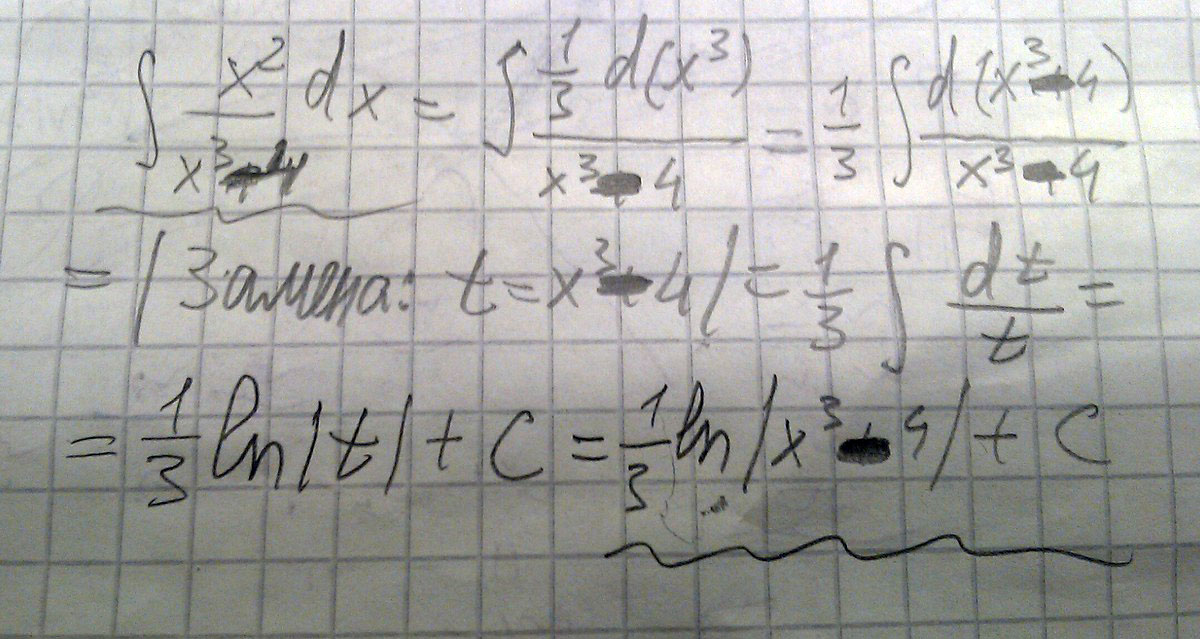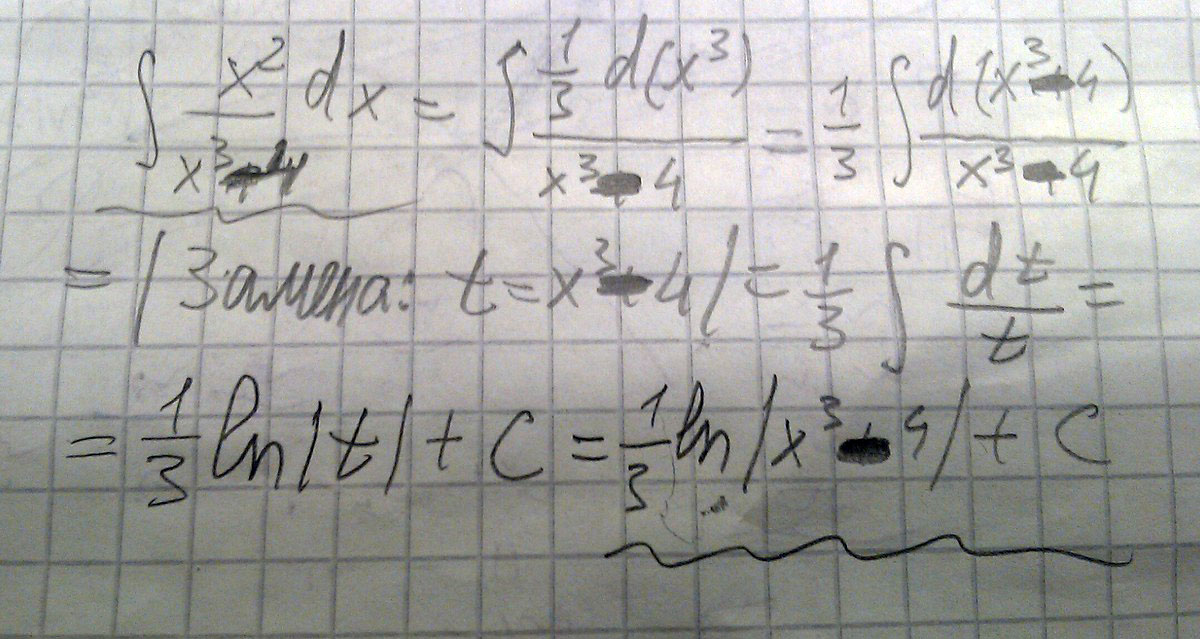интеграл »
найти интеграл - страница 12
Интеграл от \( \frac{dx}{ \sqrt{x} (x+3)} \)
Решение: Ответ:$$ \frac{2}{3} \sqrt{x} *(x+9) $$Делаем замену переменной
√x=t
Дифференцируем
$$ \frac{dx}{2 \sqrt{x} } =dt \\ \frac{dx}{ \sqrt{x} }=2dt $$
Получаем
$$ \int\limits\frac{dx}{ \sqrt{x} (x+3)} = \int\limits \frac{2dt}{t^2+3} =2\int\limits \frac{dt}{t^2+( \sqrt{3} )^2} = \\ =2 *\frac{1}{ \sqrt{3} } arctg \frac{t}{ \sqrt{3} } +C $$
Возвращаемся к старой переменной х:
$$ \frac{2}{ \sqrt{3} } arctg \frac{ \sqrt{x} }{ \sqrt{3} } +C $$
ИНТЕГРАЛ ОТ: \( \frac{2 x^{2} -5x+1 }{ x^{3} -2 x^{2} +1} dx \)
Решение: $$ \frac{2x^2-5x+1}{x^3-2x^2+1} = \frac{2x^2-5x+1}{(x-1)(x^2-x-1)}=\frac{2x^2-5x+1}{(x-1)(x-\frac{1-\sqrt5}{2})(x- \frac{1+\sqrt5}{2} )} =\\\\= \frac{A}{x-1}+\frac{B}{x-\frac{1-\sqrt5}{2}}+\frac{C}{x-\frac{1+\sqrt5}{2}} \; ;\\\\2x^2-5x+1=A(x-\frac{1-\sqrt5}{2})(x-\frac{1+\sqrt5}{2}{})+B(x-1)(x-\frac{1+\sqrt5}{2})+\\\\+C(x-1)(x- \frac{1-\sqrt5}{2} )\; ; \\ x=1:\; \; A= \frac{-2}{(1- \frac{1-\sqrt5}{2})(1-\frac{1+\sqrt5}{2})}=\frac{-2}{-1} =2\\\\x= \frac{1-\sqrt5}{2} ;\; \; B= \frac{(3+3\sqrt5)/2}{(5+\sqrt5)/2}=\frac{3}{\sqrt5} \\ x= \frac{1+\sqrt5}{2} :\; \; C= \frac{(3-3\sqrt5)/2}{\sqrt5(\sqrt5-1)/2} =-\frac{3}{\sqrt5}\; ;\\\\\\\int \frac{2x^2-5x+1}{x^3-2x^2+1} dx=2\int \frac{dx}{x-1}+\frac{3}{\sqrt5}\int \frac{dx}{x-\frac{1-\sqrt5}{2}}-\frac{3}{\sqrt5}\int \frac{dx}{x-\frac{1+\sqrt5}{2}} =\\\\=2ln|x-1|+\frac{3}{\sqrt5}\cdot ln\left |x-\frac{1-\sqrt5}{2}\right |-\frac{3}{\sqrt5}\cdot ln\left |x-\frac{1+\sqrt5}{2}\right |+C $$
(x^3 dx)/(〖(5x〗^4+3)〖^5〗) решите интеграл
Решение:
interpret. (x^3 dx)/( ( [5x]^4+3) [^5] ). $$ \Rightarrow \int{ \frac{ x^3 dx }{ ( (5x)^4 + 3 )^5 } } = \frac{1}{5^4} \int{ \frac{ (5x)^3 d (5x) }{ ( (5x)^4 + 3 )^5 } } = \\ = \frac{1}{ 4 \cdot 5^4 } \int{ \frac{1}{ ( (5x)^4 + 3 )^5 } } \, \cdot 4 \cdot (5x)^3 d (5x) = \frac{1}{ 4 \cdot 5^4 } \int{ \frac{1}{ ( (5x)^4 + 3 )^5 } } \, d (5x)^4 = \\\\ = \frac{1}{ 4 \cdot 5^4 } \int{ \frac{ d ( (5x)^4 + 3 ) }{ ( (5x)^4 + 3 )^5 } } = \frac{1}{ 4 \cdot 5^4 } \int{ ( (5x)^4 + 3 )^{-5} } \, d ( (5x)^4 + 3 ) = \\\\ = \frac{1}{ 1 + [- 5] } \cdot \frac{1}{ 4 \cdot 5^4 } \cdot ( (5x)^4 + 3 )^{-4} + C = \frac{1}{4} \cdot \frac{1}{ 4 \cdot 5^4 } \cdot \frac{1}{ ( (5x)^4 + 3 )^4 } + C = \\\\ = \frac{1}{ 2^2 \cdot 2^2 \cdot 5^4 } \cdot \frac{1}{ ( (5x)^4 + 3 )^4 } + C = \frac{1}{ 2^4 \cdot 5^4 } \cdot \frac{1}{ ( (5x)^4 + 3 )^4 } + C = \frac{1}{ 10^4 } \cdot \frac{1}{ ( (5x)^4 + 3 )^4 } + C \ ; $$
О т в е т : $$ \int{ \frac{ x^3 dx }{ ( (5x)^4 + 3 )^5 } } = \frac{1}{ 10 \ 000 \ ( (5x)^4 + 3 )^4 } + C \. $$
Интеграл
( arctg^(37/60) (x^4+5) ) / (x^5 + 10x + 26/x^3 )
Решение: $$ \int {\frac{\sqrt[60]{arctg^{37} \, (x^4+5) }}{x^5 +10x +\frac{26}{x^3}}} \, dx = \int {\frac{x^3 \cdot arctg^{\frac{37}{60}} \, (x^4+5) }{x^8 +10x^4 +26}} \, dx=(*) \\ \\ t=arctg(x^4+5); \ \ dt = \frac{4x^3 \, dx}{1+x^8+10x+25}; \ \ dx= \frac{x^8 +10x+26 }{4x^3}\, dt \\ \\ (*) = \int {\frac{x^3 \cdot t^\frac{37}{60}}{x^8 +10x+26 } \cdot \frac{x^8 +10x+26 }{4x^3}\, dt =\frac{1}{4} \int {t^\frac{37}{60}} \, dt=\frac{1}{4 } \cdot \frac{60}{97} \cdot t^\frac{97}{60}+C}= \\ \\ \\ = \frac{15}{97} \cdot arctg^\frac{97}{60} \, (x^4+5)+C $$
Интеграл. в числителе x^2 dxВ знаменатели x^3-4
Решение: $$ \int{\frac{x^2dx}{x^3-4}}=\\ \|dx^3=3x^2dx==>x^2dx=\frac13dx^3\|\\ =\int{\frac{\frac13dx^3}{x^3-4}}=\frac13\int{\frac{dx^3}{x^3-4}}=\\ \|d(x^3-4)=dx^3\| =\frac13\int{\frac{d(x^3-4)}{x^3-4}}=\\ \|x^3-4=p;d(x^3-4)=dp\|\\ =\frac13\int{\frac{dp}{p}}=\frac13\cdot\ln|p|+C=\frac13\ln|x^3-4|+C $$