интеграл »
найти интеграл - страница 13
Интеграл\( \int\limits x^{6}*(x^{7}-3) \ \, dx \)
Решение: Раскроем скобки под интегралом:
∫(х^13 -3*x^6)dx
Интеграл разности равен разности интегралов, т. е.:
∫х^13 dx -∫3*x^6dx
Константу из под интеграла можно безопасно вынести:
∫х^13 dx -3∫x^6dx
Найдём интегралы по 3ей формуле из прилагаемой таблицы интегралов:
$$ \frac{x^{14} }{14} + C_{1} - 3* \frac{ x^{7} }{7} + C_{2} = \frac{x^{14} }{14} - 3* \frac{ x^{7} }{7} + C $$
С1 и С2 мы объединили в одну константу "С".
Найдите интеграл и вычичлить S(x^4-8x^3+4x)dx
Решение: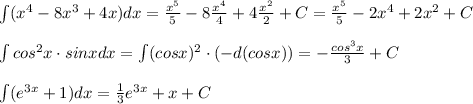
Решить: 1)S(интеграл) 3cos xdx
2)S 10*2^x dx
3)S 4dx/1+x^2
Решение: Помогите решить и объясните
1)$$ \int\limits{3cos(x)} \, dx $$
2)$$ \int\limits{10*2^{x}} \, dx $$
3)$$ \int\limits{ \frac{4}{1+x^2}} \, dx $$
Решение:
Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла
$$ \int\limits{C*f(x)} \, dx = C*\int\limits{f(x)} \, dx $$
где C-константа(не равная нулю)
$$ 1) \int\limits{3cos(x)} \, dx = 3\int\limits{cos(x)} \, dx=-3sin(x)+C \\ 2) \int\limits{10*2^{x}} \, dx =10 \int\limits{2^{x}} \, dx= \frac{10*2^x}{ln(2)}+C \\ 3) \int\limits{ \frac{4}{1+x^2}} \, dx= 4\int\limits{ \frac{1}{1+x^2}} \, dx=4arctg(x)+C $$
На рисунке изображен график некоторой функции y=f(x). Пользуясь рисунком, вычислите определенный интеграл от 4 до -2 f(x)dx.
Решение: Для ответа на вопрос задания найдём площадь трапеции
Верхнее основание 4-1=3
Нижнее 4-(-2)=6
высота 3
S=(3+6):2·3=4,5·3=13,5
Ответ: интеграл равен 13,5Чтобы вычислить определенный интеграл можно рассуждать следующим образом:
1. Площадь плоской фигуры находиться с помощью определенного интеграла
Значит, если найти площадь этой фигуры, мы найдем заданный интеграл
2. Фигура состоит их треугольника и квадрата
3. Площадь треугольника равна 1/2 ·3·3=4,5
4. Площадь квадрата равна 3·3=9
5. S·= 4,5+9 = 13,5 (кв. ед.)
Решите интегралы: \( 1)\; \int \frac{x^4}{x^2+3}dx\\ 2)\; \int (e^{x}+x)^2dx\\ 3)\; \int \frac{dx}{sinx}\\ 4)\; \int_0^{\frac{\pi}{2}}sinx\cdot cos^2x\, dx \)
Решение: $$ 1)\; \int \frac{x^4}{x^2+3}dx=\int (x^2-3+\frac{9}{x^2+3})dx=\frac{x^3}{3}-3x+9\cdot \frac{1}{\sqrt3}arctg\frac{x}{\sqrt3}+C\\\\2)\; \int (e^{x}+x)^2dx=\int (e^{2x}+2xe^{x}+x^2)dx=I\\\\\int xe^{x}dx=[u=x,\; du=dx,\; dv=e^{x}dx,\; v=e^{x}]= uv-\int vdu=\\\\=xe^{x}-\int e^{x}dx=xe^{x}-e^{x}+C_1=e^{x}(x-1)+C_1\\\\I=\frac{1}{2}e^{2x}+2e^{x}(x-1)+\frac{x^3}{3}+C \\ 3)\; \int \frac{dx}{sinx}=\int \frac{sinx}{sin^2x}dx=\int \frac{-d(cosx)}{1-cos^2x}=[t=cosx,\; dt=-sinx\, dx]=\\\\=-\int \frac{dt}{1-t^2}=\int \frac{dt}{t^2-1}=\frac{1}{2}ln|\frac{t-1}{t+1}|+C=\\=\frac{1}{2}ln|\frac{cosx-1}{cosx+1}|+C=ln|tg\frac{x}{2}|+C \\ 4)\; \int_0^{\frac{\pi}{2}}sinx\cdot cos^2x\, dx=\\\\=[t=cosx,dt=-sinx\, dx,\; \int t^2\cdot (-dt)=-\frac{t^3}{3}+C]=\\\\=-\frac{cos^3x}{3}|_0^{\frac{\pi}{2}}=-\frac{1}{3}(cos\frac{\pi}{2}-cos0)=-\frac{1}{3}(0-1)=\frac{1}{3} $$