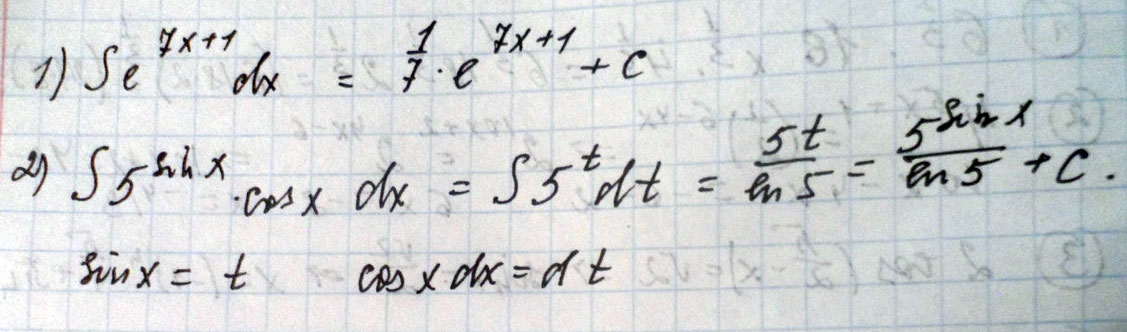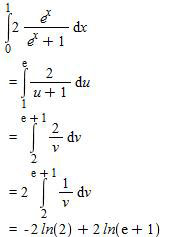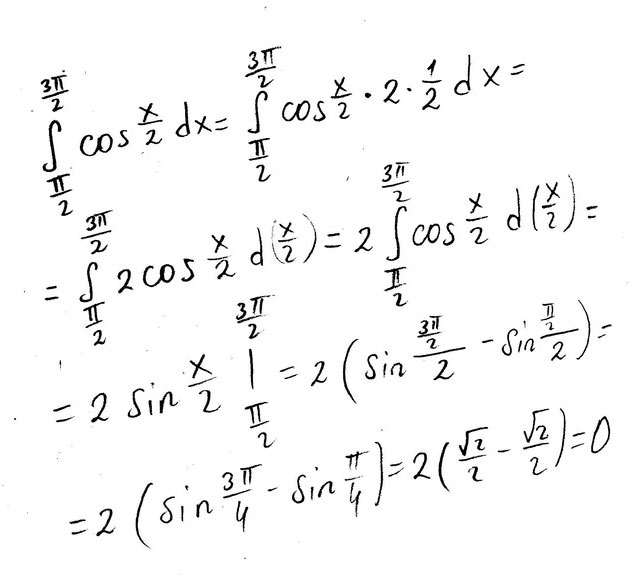интеграл »
найти интеграл - страница 14
Найти интегралы \( \int \:e^{7x+1}dx \\ \int \:5^{\sin \left(x\right)}\cos \left(x\right)dx \)
Решение: $$ \int \:e^{7x+1}dx = [ u=7x+1,\quad \quad du=7dx,\:\quad \:dx=\frac{1}{7}du ] =\\= \int \frac{e^u}{7}du =\\= \frac{1}{7}e^u =\\= \frac{1}{7}e^{\left(7x+1\right)} =\\= \frac{e^{7x+1}}{7}+C \\ \int \:5^{\sin \left(x\right)}\cos \left(x\right)dx =\\= [ u=\sin \left(x\right),\quad \quad du=\cos \left(x\right)dx,\:\quad \:dx=\frac{1}{\cos \left(x\right)}du ] =\\= \int \:5^u\cos \left(x\right)\frac{1}{\cos \left(x\right)}du =\\= \int \:5^udu =\\= \frac{5^u}{\ln \left(5\right)} =\\= \frac{5^{\sin \left(x\right)}}{\ln \left(5\right)}+C $$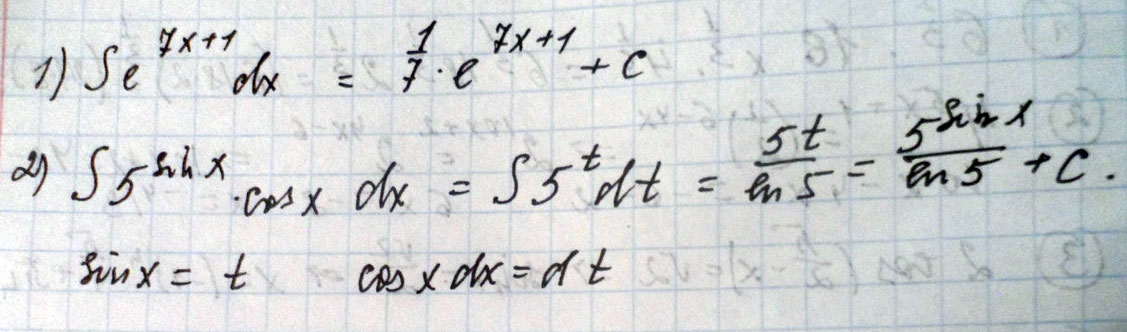
Вычисление неопределённых интегралов. \( \int\limits( {3x^8- \frac{3}{x^3}+4x+9) } \, dx\\ \int\limits {(7e^{2x}-5sin \frac{x}{2}+6x-9) } \\ dx\\ \int\limits{ \frac{dx}{ \sqrt{2-3x} } } \, dx\\ \int\limits{ \frac{2e^x}{(5+e^x)^2} } \, dx\\ \int\limits{ \frac{cosx}{ \sqrt{1+sinx} } } \, dx \\ \int\limits{ \frac{arctg^4x}{x^2+1} } \, dx \)
Решение: $$ \int\limits( {3x^8- \frac{3}{x^3}+4x+9) } \, dx= 3\int\limits{x^8} \, dx -3 \int\limits{ \frac{1}{x^3} } \, dx +4 \int\limits {x} \, dx+9 \int\limits {} \, dx = \\ 3 \frac{x^9}{9}-3*(- \frac{1}{2x^2})+4 \frac{x^2}{2}+9x= \frac{x^9}{3}+ \frac{3}{2x^2}+2x^2+9x= \\ \frac{1}{6x^2}(2x^3(x^8+6x+27)+9+const \\ \int\limits {(7e^{2x}-5sin \frac{x}{2}+6x-9) } \, dx =7 \int\limits{e^2x} \, dx-5 \int\limits{sin \frac{x}{2} } \, dx+6 \int\limits{x} \, dx- \\ 9 \int\limits{} \, dx= \frac{7e^{2x}}{2}-10cos \frac{x}{2}+ 3x^2-9x+const \\ \int\limits{ \frac{1}{ \sqrt{2-3x} } } \, dx $$
пусть $$ u=2-3x $$, тогда $$ du=-3dx $$ подставляем $$ - \frac{du}{3} $$
$$ \int\limits{ \frac{1}{ \sqrt{u} } } \, du=- \frac{2 \sqrt{u} }{3} $$
проводим обратную замену $$ - \frac{2 \sqrt{2-3x} }{3}+const \\ \int\limits{(x^4+3)^5x^3} \, dx $$
пусть $$ u=x^4+3 $$, тогда $$ du=4x^3dx $$ подставляем $$ \frac{du}{4} \\ \int\limits { \frac{1}{4}u^5} \, du = \frac{1}{4} \int\limits{u^5} \, du = \frac{u^6}{4*6}= \frac{u^6}{24} $$
проводим обратную замену $$ \frac{(x^4+3)^6}{24}+const \\ \int\limits{ \frac{2e^x}{(5+e^x)^2} } \, dx = $$
пусть $$ u=e^x $$, тогда $$ du=e^xdx $$ подставим $$ 2du \\ 2 \int\limits{ \frac{1}{u^2+10u+25} } \, du=2 \int\limits{ \frac{1}{(u+5)^2} } \, du $$
проведем вторую замену пусть $$ y=u+5 $$, тогда $$ dy=du $$ подставляем $$ \int\limits{ \frac{1}{y^2} } \, dy =- \frac{1}{y} $$
проводим обратную замену $$ - \frac{1}{u+5} $$ проводим вторую обратную замену $$ - \frac{2}{e^x+5}+const \\ \int\limits{ \frac{cosx}{ \sqrt{1+sinx} } } \, dx = $$
пусть $$ u=sinx+1 $$, тогда$$ du=cosxdx $$ подставим $$ \int\limits{ \frac{1}{ \sqrt{u} } } \, du=2 \sqrt{u} $$
проводим обратную замену $$ 2 \sqrt{sin(x)+1} +const \\ \int\limits{ \frac{arctg^4x}{x^2+1} } \, dx $$
пусть $$ u=arctg(x) $$ тогда $$ du= \frac{dx}{x^2+1} $$ подставляем
$$ \int\limits{u^4} \, du = \frac{u^5}{5} $$
проводим обратную замену переменной
$$ \frac{arctg^5(x)}{5}+const $$
Интеграл, нижний предел 0, верхний 1. (2e^x*dx) / (e^x+1)
Решение: Две замены переменных, потом интеграл от степенной функции или дроби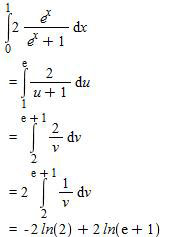
Нижний предел интегрирования П/2
Верхний предел 3П/2
Сам интеграл:cos(x/2)*dx
Решение: Решение в приложении. Ответ: 0.$$ \int _{\frac{\pi}{2}}^{\frac{3\pi}{2}}\, cos\frac{x}{2}dx=2sin\frac{x}{2}|_{\frac{\pi}{2}}^{\frac{3\pi}{2}}=2(sin\frac{3\pi}{4}-sin\frac{\pi}{4})=2(\frac{\sqrt2}{2}-\frac{\sqrt2}{2})=0 $$
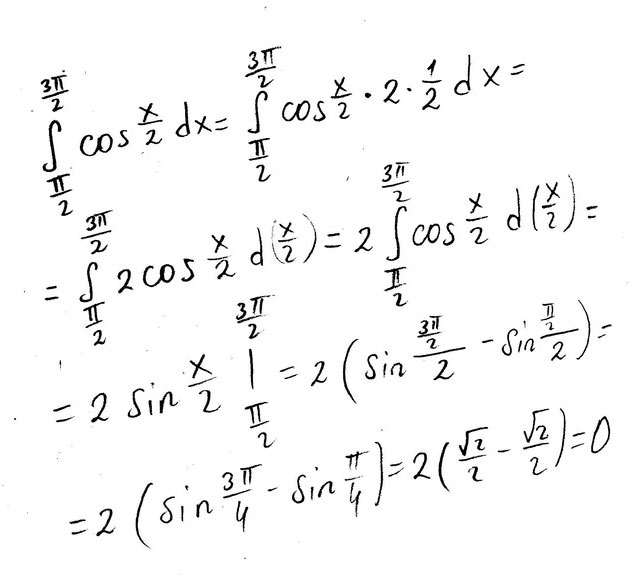
ИНТЕГРАЛ dx/((x^1/2)-(x^1/4))
Решение: Замена переменной:
х=t⁴
dx=4t³dt
√x=t²
$$ \sqrt[4]{x}=t \\ \int\limits { \frac{dx}{ \sqrt{x} - \sqrt[4]{x} } } \, = \int\limits { \frac{4t ^{3}dt}{t ^{2}-t } } \, = \\ = 4\int\limits { \frac{t\cdot t ^{2} }{t(t-1)} } \, dt =4 \int\limits { \frac{t ^{2}-1+1 }{t-1} } \, dt= $$
=$$ =4 \int\limits {(t+1+ \frac{1}{t-1}) } \, dt=4t ^{2} +4t+4ln|t-1|+C= $$
=обратная замена=
=$$ =4 \sqrt{x} +4 \sqrt[4]{x} +4 ln | \sqrt[4]{x}-1|+C $$