модуль »

как найти модуль - страница 7

  • |х²-5х| = х + 16 Модуль)))


    Решение: |х²-5х|=х+16
    1) х²-5х=х+16
    х²-5х-х-16=0
    х²-6х-16=0
    D=b²-4ac=36+64=100
    x1=-b+√D/2a=6+10/2=16/2=8
    x2=-b-√D/2a=6-10/2=-4/2=-2
    2) -x²+5x=x+16
    -x²+5x-x-16=0
    -x²+4x-16=0
    x²-4x+16=0
    D=b²-4ac=16-64=-48<0 корней нет
    Ответ: х=8, х=-2

    х - х х х - х х х - х-х- х - х- D b - ac x -b D a x -b- D a - - - -x x x -x x-x- -x x- x - x D b - ac - - lt корней нетОтвет х х -...

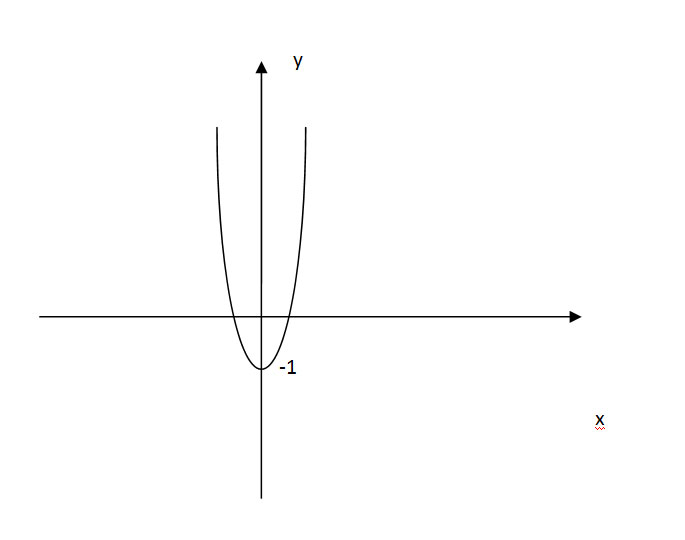
  • У=х^2+2|x|-1 для х больше или равно 0, там модуль раскрывается и х0(координата) получается отрицательная=-1


    Решение: 1)x<0
    y=x²-2x-1=(x-1)²-2
    Парабола у=х², вершина (1:-2). Строится только при х<0
    2)x≥0
    y=x²+2x-1=(x+1)²-2
    Парабола у=х², вершина (-1:-2). Строится только при х≥0

    x...

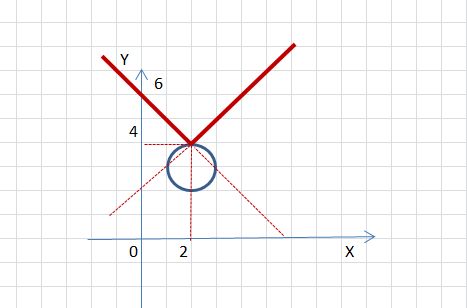
  • Решить графически систему: х^2+y^2+12=4x+6y

    y+|х-2|=4

    |. модуль


    Решение: преобразуем: х^2+y^2+12=4x+6y

    х^2-4х+4+y^2-6у+9=4+9-12

    (х-2)^2+(y-3)^2=1 окружность с радиусом 1 и центром в точке (2;3)

    преобразуем: y+|х-2|=4

    y=-|х-2|+4

    при x>=2 y=-x+6

    при x<2  y=x+2

    Решение: точка (2;4)

    преобразуем х y x y х - х y - у - х- y- окружность с радиусом и центром в точке преобразуем y х- y - х- при x gt y -x при x lt   y x Решение точка...

  • 1) три умноженное на модуль числа икс равно шестнадцати

    3 умноженное на /х/ = 16

    2) сто семь минус 2 умноженное на модуль числа икс равно тридцать один

    107-2х/х/ =31

    3) модуль числа икс плюс шесть равен тринадцати

    /х/ + 6 = 13

    4) пять минус две целых пять десятых умноженное на модуль числа икс равно семи

    5-2,5х /х/ = 7

    5) три плюс 2 модуль числа минус икс равно одному

    3+2 /-х/ = 1

    6) одиннадцать плюс четыре модуль два икс минус один равно трем

    11+4 /2x - 1/ = 3


    Решение: 1) три умноженное на модуль числа икс равно шестнадцати3 умноженное на  /х/ = 16
    !X!=16/3
    x=16/3
    x=-16/3
    2) сто семь минус 2 умноженное на модуль числа икс равно тридцать один107-2х/х/ =31
    x<0
    107+2x^2=31 решений нет
    x>=0
    107-2x^2=31
    x^2=38
    x=корень(38)
    3) модуль числа икс плюс шесть равен тринадцати/х/ + 6 = 13
    x<0
    -x+6=13
    x=-7
    x>=0
    x+6=13
    x=7
    4) пять минус две целых пять десятых умноженное на модуль числа икс равно семи5-2,5х /х/ = 7
    x<0
    5+2.5x^2=7
    2.5x^2=2
    x^2=4/5
    x=-корень(4/5)
    x>0
    5-2ю5x^2=7
     нет решений
    5) три плюс 2 модуль числа минус икс равно одному3+2 /-х/ = 1
    2!x!=-2 решений нет модуль положителен всегда

  • Решите: 2|x - 1| + 3|x + 2| = 17


    Решение: 2|х-1|+3|х+2|=17
    рассмотрим все значения когда раскрываются модули
                           ! х-1! х+2!
    x<-2            1-x                  -x-2
    -2<=x<=1       1-x                 x+2
    x>1                 x-1                 x+2
    x<-2
    2! х-1!+3! х+2!=17
    2(1-x)-3(x+2)=17
    2-2x-3x-6=17
    -5x=21
    x=-21/5 это меньше -2
    -2<=x<=1
    2! х-1!+3! х+2!=17
    2(1-x)+3(x+2)=17
    2-2x+3x+6=17
    x=9 корень не попадает в интервал
    x>1
    2! х-1!+3! х+2!=17
    2(x-1)+3(x+2)=17
    2x-2+3x+6=17
    5x=13
    x=13/5 корень попадает в интервал. Ответ: 13/5,21/5

<< < 567 8 9 > >>