НОД и НОК »
найдите наименьшее общее кратное - страница 11
Найдите наименьшее общее кратное натуральных чисел представленных в виде произведения простых множителей
Решение: Допустим, нужно найти НОК чисел 6 и 4. Для этого представим их в виде произведения простых множителей так, чтобы один из них был общим, то есть $$ 6=2*3,4=2*2 $$. Мы видим, что 2 есть и в числе 6 и 4, значит, выписываем общую для них двойку, затем числа, которые не равны двум (если повторяются, то тоже считать), то есть $$ 2*3*2=12 $$. 12 - есть НОК этих чисел.Найдите наименьшее общее кратное чисел, разложив их на простые множители
21 и 18
24 и 32
16 и 20
20 и 35
75 и 90
6 и 13
14 и 18
28 и 42
21 и 33
12,30 и 75
15,42 и 105
21,28 и 35
если можно решение полностью, а не одни ответы.
Решение: Чтобы найти НОК нескольких чисел, нужно разложить их на простые множители и найти произведение всех простых множителей, взятых с наибольшим показателем степени.
21 = 3 * 7 18 = 2 * 3 * 3
НОК (21 и 18) = 2 * 3 * 3 * 7 = 126 - наименьшее общее кратное
24 = 2 * 2 * 2 * 3 32 = 2 * 2 * 2 * 2 * 2
НОК (24 и 32) = 32 * 3 = 96 - наименьшее общее кратное
16 = 2 * 2 * 2 * 2 20 = 2 * 2 * 5
НОК (16 и 20) = 16 * 5 = 80 - наименьшее общее кратное
20 = 2 * 2 * 5 35 = 5 * 7
НОК (20 и 35) = 2 * 2 * 5 * 7 = 140 - наименьшее общее кратное
75 = 3 * 5 * 5 90 = 2 * 3 * 3 * 5
НОК (75 и 90) = 2 * 3 * 3 * 5 * 5 = 450 - наименьшее общее кратное
6 = 2 * 3 13 - простое число
НОК (6 и 13) = 6 * 13 = 78 - наименьшее общее кратное
14 = 2 * 7 18 = 2 * 3 * 3
НОК (14 и 18) = 2 * 3 * 3 * 7 = 126 - наименьшее общее кратное
28 = 2 * 2 * 7 42 = 2 * 3 * 7
НОК (28 и 42) = 2 * 2 * 3 * 7 = 84 - наименьшее общее кратное
21 = 3 * 7 33 = 3 * 11
НОК (21 и 33) = 3 * 7 * 11 = 231 - наименьшее общее кратное
12 = 2 * 2 * 3 30 = 2 * 3 * 5 75 = 3 * 5 * 5
НОК (12; 30 и 75) = 2 * 2 * 3 * 5 * 5 = 300 - наименьшее общее кратное
15 = 3 * 5 42 = 2 * 3 * 7 105 = 3 * 5 * 7
НОК (15; 42 и 105) = 2 * 3 * 5 * 7 = 210 - наименьшее общее кратное
21 = 3 * 7 28 = 2 * 2 * 7 35 = 5 * 7
НОК (21,28 и 35) = 2 * 2 * 3 * 5 * 7 = 420 - наименьшее общее кратное
Найдите наименьшее общее кратное чисел, разломив их на простые множители;
21и 18 20и 35
24 и 32 75 и 90
16 и 20 6 и 13
Решение: 1. 126 2. 140 3. 96 4. 450 5. 80 6. 78HOD(21 и 18)=3
21=3•7;-вычёркиваем 7
18=2•3•3.
21|3. 18|2
7|7 9|3
1|. 3|3
1
НОD(24 и 32)=8
24=2•2•2•3-вычёркиваем 3
32=2•2•2•2•2
24|2. 32|2
12|2. 16|2
6|2. 8|2
3|3. 4|2
1. 2|2
1
HOD(16 и 20)=4
16=2•2•2•2-вычёркиваем 2 и 2
20=2•2•5
16|2. 20|2
8|2. 10|2
4|2. 5|5
2|2. 1
1
Найдите наименьшее общее кратное чисел 2и5 3и4 нод
Решение: 3 и4 :общие кратное число 12
12и18:
общие кратное 36
16и 3:
общие кратное число 48
30 и 45:
общие кратное число 90
Вот. вот. вот.
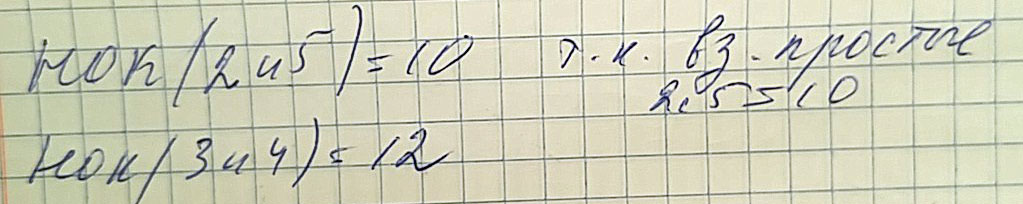
Найдите наименьшее общее кратное чисел 28. 35 и 70 36. 54 и 82 25.75 и150
Решение: 28 = 2 * 2 * 7
35 = 5 * 7
70 = 2 * 5 * 7
НОК (28; 35 и 70) = 2 * 2 * 5 * 7 = 140 - наименьшее общее кратное
140 : 28 = 5 140 : 35 = 4 140 : 70 = 2
36 = 2 * 2 * 3 * 3
54 = 2 * 3 * 3 * 3
82 = 2 * 41
НОК (36; 54 и 82) = 2 * 2 * 3 * 3 * 3 * 41 = 4428 - наименьшее общее кратное
4428 : 36 = 123 4428 : 54 = 82 4428 : 82 = 54
25 = 5 * 5
75 = 3 * 5 * 5
150 = 2 * 3 * 5 * 5
НОК (25; 75 и 150) = 2 * 3 * 5 * 5 = 150 - наименьшее общее кратное
150 : 25 = 6 150 : 75 = 2 150 : 150 = 1

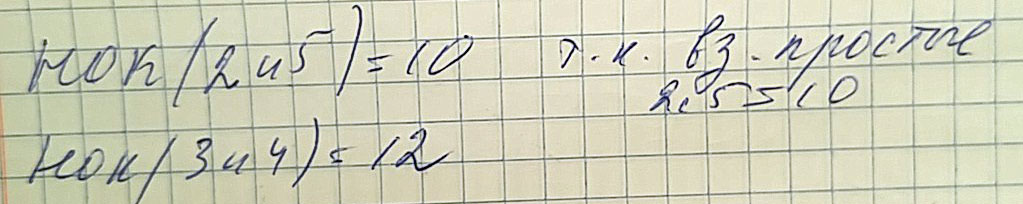
 Возьмём три числа: 60, 90 и 120. Каждое из них делится на 30. Значит число 30 есть делитель каждого из них. Принято говорить, что число 30 есть общий делитель чисел: 60, 90 и 120.
В дальнейшем нам часто придётся искать общий делитель для двух, трёх и т. д. чисел. Запомним, что общим делителем нескольких чисел называется число, на которое все данные...
Возьмём три числа: 60, 90 и 120. Каждое из них делится на 30. Значит число 30 есть делитель каждого из них. Принято говорить, что число 30 есть общий делитель чисел: 60, 90 и 120.
В дальнейшем нам часто придётся искать общий делитель для двух, трёх и т. д. чисел. Запомним, что общим делителем нескольких чисел называется число, на которое все данные...