НОД и НОК »
найти наибольший общий делитель - страница 7
найти наибольший общий делитель и наименьшее общее кратное чисел 504 и 756
Решение: Для того чтобы найти наибольший общий делитель необходимо разложить каждое из заданных чисел на простые множители. Потом выписать отдельно только те множители которые входят во все заданные числа. Потом перемножить между собой выписанные числа.504 = 2³ · 3² · 7
756 = 2² · 3³ · 7
наибольший общий делитель(504;756) = 2² · 3² · 7 = 252Чтобы найти наименьшее общее кратное заданных чисел, нужно выписать все простые множители, входящие хотя бы в одно из данных чисел, каждый из взятых множителей возвести в наибольшую из тех степеней, с которыми он входит в заданные числа и их перемножить.
504 = 2³ · 3² · 7
756 = 2² · 3³ · 7
Наименьшее общее кратное(504;756) = 2³ · 3³ · 7 = 1512
Найти Наибольший общий делитель чисел k и l. Если их произведение равно 82.800, а Наибольшее общее кратное рано 1380
Решение: Наибольшее общее кратное? Скорее наименьшее, так как наибольшего не существует, оно в пределах бесконечности.
Нам дано произведение и НОК.
НОК = 1380. НОК может быть равен одному из двух чисел. Так и представим, что k=1380. 82800 - произведение
l = 82800 / 1380
l = 60
Теперь надо найти наибольший общий делитель - НОД.
И НОД будет равен 60. 1380 делится на 60 без остатка и 60 на 60 без остатка. В других случаях будет либо дробное значение (с остатком) или будет не наибольшее.
Ответ - 60Найдите наибольший общий делитель и наименьшее общее кратное чисел 504 и 756
Решение: 504 = 2 * 2 * 2 * 3 * 3 * 7756 = 2 * 2 * 3 * 3 * 3 * 7
НОД (504 и 756) = 2 * 2 * 3 * 3 * 7 = 252 - наибольший общий делитель
504 : 252 = 2 756 : 252 = 3
НОК (504 и 756) = 2 * 2 * 2 * 3 * 3 * 3 * 7 = 1512 - наименьшее общее кратное
1512 : 504 = 3 1512 : 756 = 2
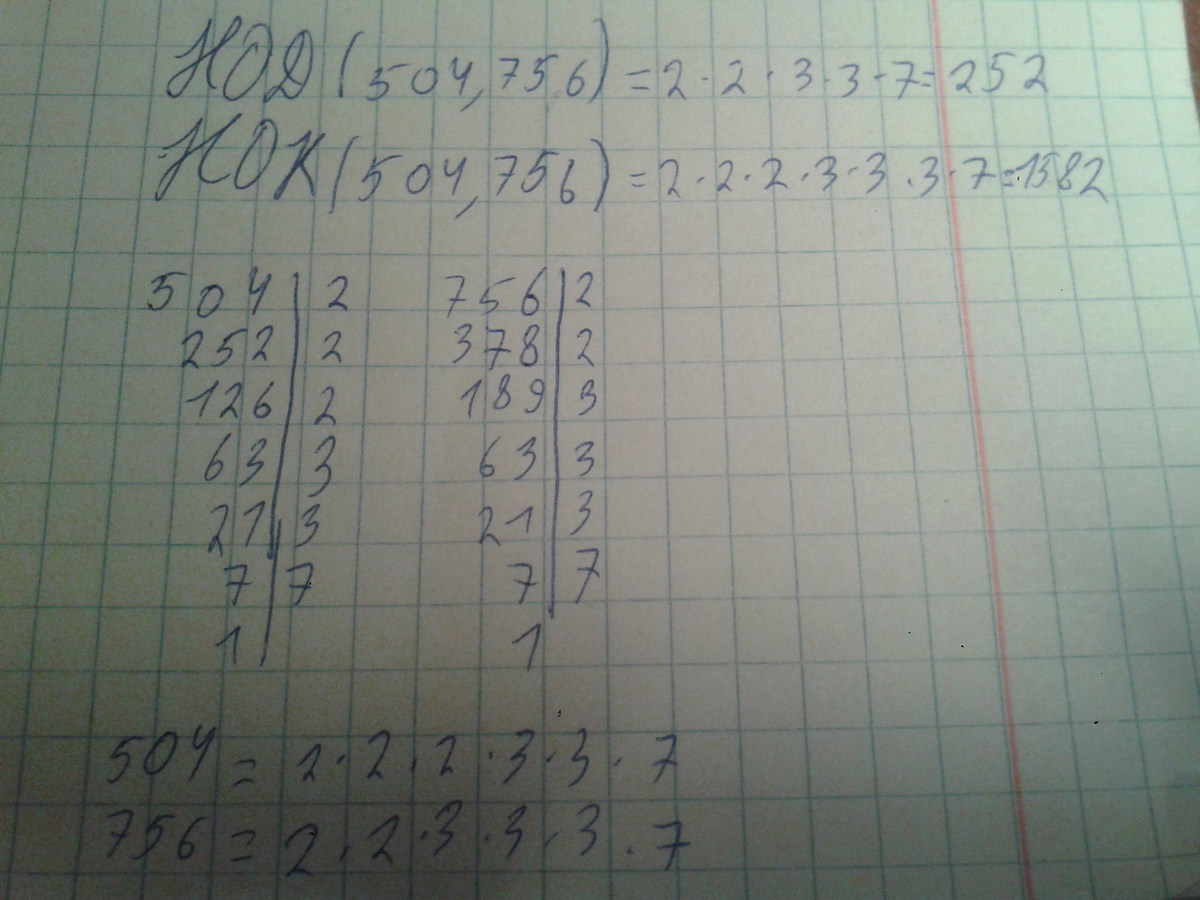
Найдите наибольший общий делитель и наименьшее общее кратное чисел: 1) 4и10; 2) 6и14; 3) 8и12; 4) 15и18; 5) 20и24; 6) 26и39.
Решение: Разложили на множители.
Для НОК берем все-все.
Для НОД - только общие
1) 4 = 2*2 и 10 = 2*5 и НОД=2 и НОК = 2*2*5 = 20
2) 6 = 2*3 и 14 = 2*7 и НОД=2 и НОК = 2*3*7 = 42
3) 8 = 2*4 и 12 = 3*4 и НОД=4 и НОК =2*3*4 = 28
4) 15 = 3*5 и 18 = 2*3*3 и НОД = 3 и НОК = 18*5 = 90
5) 20 = 4*5 и 24 = 4*6 и НОД = 4 и НОК = 4*5*6 = 120
6) 26 = 2*13 и 39 = 3*13 и НОД = 13 и НОК = 6*13 = 78.Найдите наибольший общий делитель и наименьший общее кратное чисел:
А: 18 и 36
Б: 33 и 44
В: 378 и 441
Г: 11.340 и 37.800
Решение: А. 18 = 2 * 3 * 3 36 = 2 * 2 * 3 * 3
НОД (18 и 36) = 2 * 3 * 3 = 18 - наибольший общий делитель
НОК (18 и 36) = 2 * 2 * 3 * 3 = 36 - наименьшее общее кратное
Б. 33 = 3 * 11 44 = 2 * 2 * 11
НОД (33 и 44) = 11 - наибольший общий делитель
НОК (33 и 44) = 2 * 2 * 3 * 11 = 132 - наименьшее общее кратное
В. 378 = 2 * 3 * 3 * 3 * 7 441 = 3 * 3 * 7 * 7
НОД (378 и 441) = 3 * 3 * 7 = 63 - наибольший общий делитель
НОК (378 и 441) = 2 * 3 * 3 * 3 * 7 * 7 = 2 646 - наименьшее общее кратное
Г. 11 340 = 2 * 2 * 3 * 3 * 3 * 3 * 5 * 7
37 800 = 2 * 2 * 2 * 3 * 3 * 3 * 5 * 5 * 7
НОД (11 340 и 37 800) = 2 * 2 * 3 * 3 * 3 * 5 * 7 = 3 780 - наибольший общий делитель
НОК (11 340 и 37 800) = 2 * 2 * 2 * 3 * 3 * 3 * 3 * 5 * 5 * 7 = 113 400 - наименьшее общее кратное

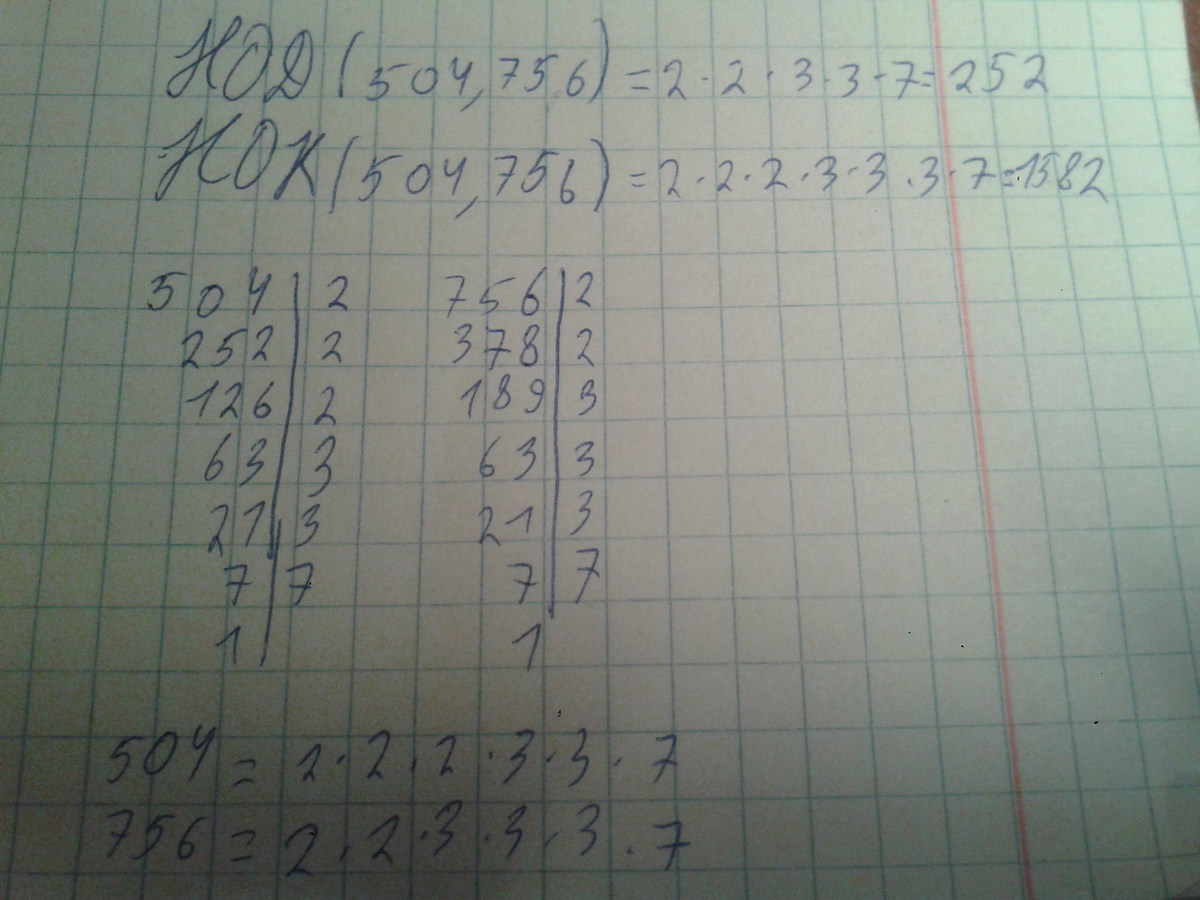
 Возьмём три числа: 60, 90 и 120. Каждое из них делится на 30. Значит число 30 есть делитель каждого из них. Принято говорить, что число 30 есть общий делитель чисел: 60, 90 и 120.
В дальнейшем нам часто придётся искать общий делитель для двух, трёх и т. д. чисел. Запомним, что общим делителем нескольких чисел называется число, на которое все данные...
Возьмём три числа: 60, 90 и 120. Каждое из них делится на 30. Значит число 30 есть делитель каждого из них. Принято говорить, что число 30 есть общий делитель чисел: 60, 90 и 120.
В дальнейшем нам часто придётся искать общий делитель для двух, трёх и т. д. чисел. Запомним, что общим делителем нескольких чисел называется число, на которое все данные...