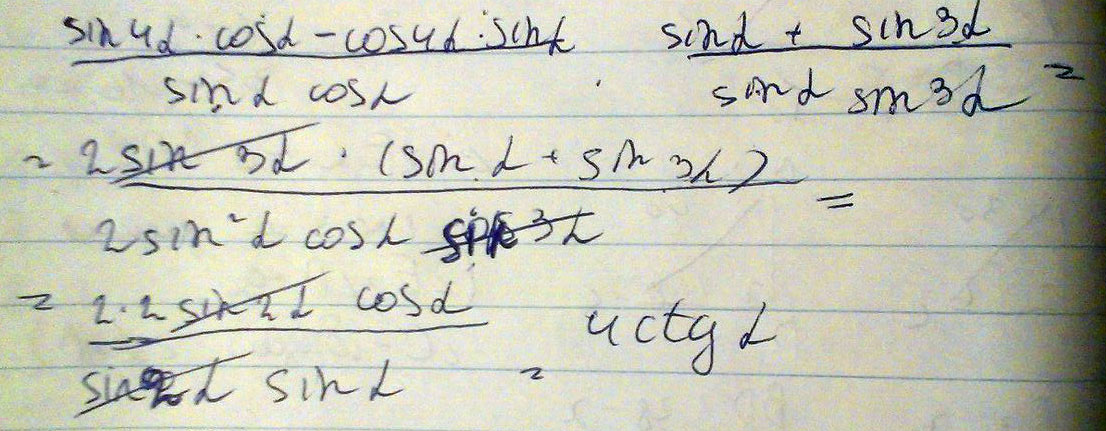тождество »

докажите тождество - страница 11

  • \( ( \frac{sin4 \alpha }{sin \alpha }- \frac{cos4 \alpha }{cos \alpha })( \frac{1}{sin3 \alpha }+ \frac{1}{sin \alpha })=4ctg \alpha \).
    Докажите тождество


    Решение: Решение на фото ниже

    1)sin4a/sina-cos4a/cosa=(sin4acosa-cosasin4a)/sinacosa=2sin(4a-a)/sin2a=
    =2sin3a/sin2a
    2)1/sin3a+1/sina=(sina+sin3a)/sinasin3a=(sina+sin3a)/sinasin3a=
    =2sin2acosa/sinasin3a
    3)2sin3a/sin2a *2sin2acosa/sinasin3a=4cosa/sina=4ctga
    4ctga=4ctga

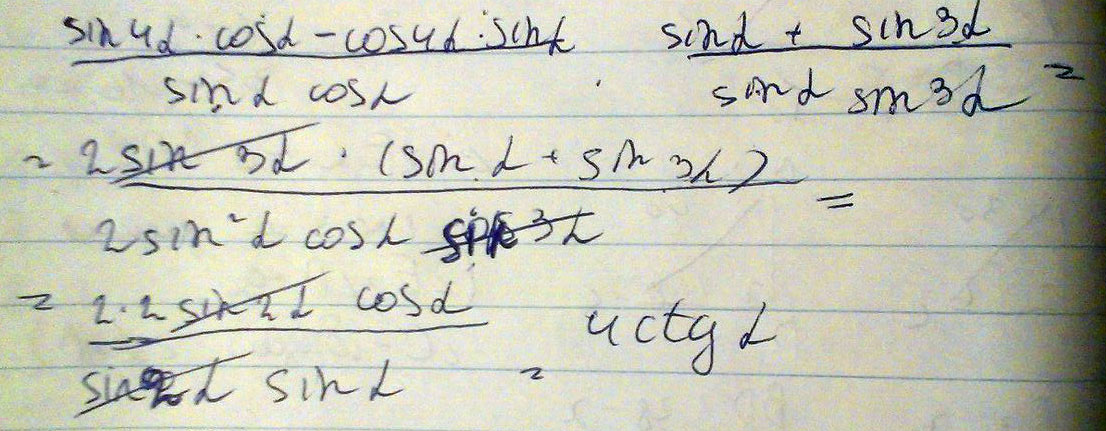
    Решение на фото ниже sin a sina-cos a cosa sin acosa-cosasin a sinacosa sin a-a sin a sin a sin a sin a sina sina sin a sinasin a sina sin a sinasin a sin acosa sinasin a sin...

  • Докажите тождество sin3a/sina - cos3a/cosa=2
    Докажите тождество cosa-cos3a/sina+sin3a=tga


    Решение: Sin3a/sina-cos3a/cosa=2
    1)Sin3a= 3sina-4sin³a
    cos3a=4cos³a-3cosa
    (3sina-4sin³a)/sina-(4cos³a-3cosa)/cosa
    sina(3-4sin²a)/sina-cosa(4cos²a-3)/cosa
    3-4sin²a-4cos²a+3=-4(sin²a+cos²a)+6=-4+6=2
    2=2
    2)cosa-cos3a/sina+sin3a=tga
    Тут опять помним чему равен синус и косинус тройного угла и в итоге получим:
    4cosa-4cos³a/4sina-4sin³a=tga
    4cosa(1-cos²a)/4sina(1-sin²a)=tga
    cosa*sin²a/sina*cos²a=tga
    Сократим и получаем доказательство :
    tga=tga

  • Докажите тождество:
    sina+sin3a+sin5a+sin7a=4cosa*cos2a*sin4a


    Решение: Здесь следует воспользоваться тригонометрическими формулами перехода от суммы к произведению:
     
    sina + sinb = 2sin(a + b)/2 * cos(a - b)/2
    cosa + cosb = 2cos(a + b)/2 * cos(a - b)/2
    sina + sin3a + sin5a + sin7a = (sin7a + sina) + (sin5a + sin3a) = 2sin4a * cos3a + 2sin4a * cosa = 2sin4a(cos3a + cosa) = 2sin4a * 2cos2a * cosa = 4cosa * cos2a * sin4a.
    Части тождества равны.
     

  • Вычислите значения: cos α, если sin α = -1/2(дробь), π < α < 3π/2
    Упростите выражения: б) 1 - sin(в квадрате)α / 1 - sin(в квадрате)α (дробь)
    г) ( ctg(в квадрате)α + 1 ) * sin(в квадрате)α - cos(в квадрате)α
    Докажите тождества: б) sin(в квадрате)α - cos(в квадрате)α + 1 = 2 sin(в квадрате)α
    г) tgα + ctgα = 1 / cosα + sinα (дробь)
    α - альфа π - число пи(180 градусов) / - дробь.


    Решение: 1) cosα = - √(1-sin²α) = -√(1- (-1/2)²) = -√(3/4) = -√3/2.
    б) (1-sin²α) /(1-sin²α) = 1;
    (1-sin²α)/(1-cos²α) =cos²α/sin²α =(cosα/sinα)² =tq²α.
    г) (ctq²α +1)*sin²α -cos²α = 1/sin²α*sin²α -cos²α =1-cos²α =sin²α.
    -
    б) sin²α -cos²α+1 =sin²α +(1-cos²α) = sin²α+sin²α =2sin²α.
    г) tqα +ctqα =sinα/cosα +cosα/sinα =(sin²α+cos²α)/sinα*α = 1/sinα*cosα
    tgα + ctgα = 1 / cosα + sinα (дробь)*
    *********************************************************
     при переходе от градусной меры (α = n°) к радианной мере :
    [ α = n/180)*π ].


  • докажите тождества cos^2fkmaf(1+tg^2альфа)-sin^2альфа=cos^2альфа


    Решение: Для удобства буду обозначать "альфа" - x (одно и тоже)

    cos^2x(1+tg^2x)-sin^2x=cos^2x

    И так, посмотрим на скобку (1+tg^2x, ее можно преобразовать 1+tg^2x=1/cos^2x)

    Получим:

    cos^2x*1/cos^2x-sin^2x=cos^2x (очевидно, что cos^2x/cos^2x=1)

    1-sin^2x=cos^2x (По основному тригонометрическому тождеству sin^2x+cos^2x=1; 1-sin^2x=cos^2x)

    cos^2x=cos^2x

    Доказано.

<< < 91011 12 13 > >>