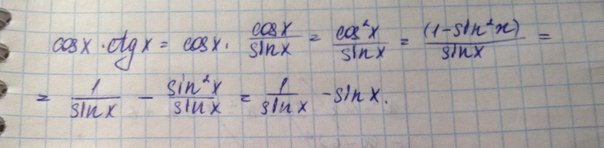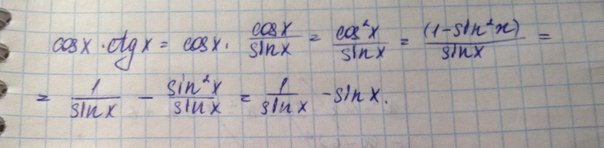тождество »
докажите тождество - страница 13
Докажите тождество: (1+sinx+cosx)/(1+sinx-cosx)=cos (x/2)
Решение: Тождество неверное.
Рассмотрим левую часть тождества.
1) Рассмотрим числитель: 1+sinx+cosx с помощью формул двойного угла можно с легкостью разложить на 2cos(x/2)(cos(x/2)+sin(x/2))
2) Рассмотрим знаменатель: 1+sinx - cosx опять таки, аналогично числителю по формулам двойного угла. Получаем: 2sin(x/2)(cos(x/2)+sin(x/2))
Откуда видим, что в левой части тождества получается ctg (x/2)
Также можно с легкостью на примере угла П/2 доказать, что тождество не верно.докажите тождество
1. 2 cos40° - cos20° / sin20° = √3
2. 2 cos80° + cos40° / sin40° = √3
Решение: 1)(-2*sin(5*пи/9)+%i*(2*cos(5*пи/9)-3*sin(4*пи/9)+4*cos(4*пи/9)+ 3*sin(2*пи/9)+2*cos(2*пи/9)+ 3*sin(пи/9)-2*cos(пи/9))-4*sin(4*пи/9)-3*cos(4*пи/9)-2*sin(2*пи/9)+3*cos(2*пи/9)+ 2*sin(пи/9)+3*cos(пи/9)-корень(3))/3 = корень(3)
2) -(i(3*sin(5*пи/9)+4*cos(5*пи/9)- 3*sin(4*пи/9)+2*cos(4*пи/9)-2*cos(2*пи/9)+ 2*cos(пи/9))-4*sin(5*пи/9)+3*cos(5*пи/9)- 2*sin(4*пи/9)-3*cos(4*пи/9)+ 2*sin(2*пи/9)-2*sin(пи/9)+корень(3))/3 = корень(3)
Докажите тождество Cos2x/1+cos2x=tgx/tg2x
Решение: $$ \frac{cos2x}{1+cos2x}=\frac{tgx}{tg2x} $$
Преобразуем правую часть в левую:
$$ \frac{tgx}{tg2x}=\frac{sinx*cos2x}{cosx*sin2x}=\frac{sinx*cos2x}{cosx*2sinx*cosx}=\frac{cos2x}{2cos^{2}x}=\frac{cos2x}{1+cos2x} $$
Использовались формулы:
1) $$ tgx= \frac{sinx}{cosx} $$
2) $$ cos2x=2cos^{2}x-1 $$, из нее следует формула: $$ 2cos^{2}x=1+cos2x $$
3) $$ sin2x=2sinx*cosx $$Докажите тождество(равенство): (1- cos2a +sin2a) / (1+ cos2a + sin2a) = tga
Решение: Выражение: (1-cos(2*x)+sin(2*x))/(1+cos(2*x)+sin(2*x))=t*g*a
Ответ: 1-2*cos(2*x)/(sin(2*x)+cos(2*x)+1)-t*g*a=0
Решаем по действиям:
1. (1-cos(2*x)+sin(2*x))/(1+cos(2*x)+sin(2*x))=1+(-2*cos(2*x)/(sin(2*x)+cos(2*x)+1))
2. 1+(-2*cos(2*x)/(sin(2*x)+cos(2*x)+1))=1-2*cos(2*x)/(sin(2*x)+cos(2*x)+1)
Решаем по шагам:
1. 1+(-2*cos(2*x)/(sin(2*x)+cos(2*x)+1))-t*g*a=0
1.1. (1-cos(2*x)+sin(2*x))/(1+cos(2*x)+sin(2*x))=1+(-2*cos(2*x)/(sin(2*x)+cos(2*x)+1))
2. 1-2*cos(2*x)/(sin(2*x)+cos(2*x)+1)-t*g*a=0
2.1. 1+(-2*cos(2*x)/(sin(2*x)+cos(2*x)+1))=1-2*cos(2*x)/(sin(2*x)+cos(2*x)+1)
Решаем уравнение 1-2*cos(2*x)/(sin(2*x)+cos(2*x)+1)-t*g*a=0:
Тестовая функция, правильность не гарантируется
Решаем относительно g:
g=-(-1+2*cos(2*x)/(sin(2*x)+cos(2*x)+1))/t/a=(1-2*cos(2*x)/(sin(2*x)+cos(2*x)+1))/t/a=(1/t-2*cos(2*x)/(sin(2*x)+cos(2*x)+1)/t)/a=(1/t-2*cos(2*x)/(sin(2*x)*t+cos(2*x)*t+t))/a=1/t/a-2*cos(2*x)/(sin(2*x)*t+cos(2*x)*t+t)/a=1/t/a-2*cos(2*x)/(sin(2*x)*t*a+cos(2*x)*t*a+t*a).
Докажите тождество 1\sinX-sinX=cosX×ctgX
Решение: Так как это тождество, то нам можно разобрать либо левую часть, либо правую.
И вот что получилось:
(см. приложение)
Левая часть равна правой.
Что и требовалось доказать.