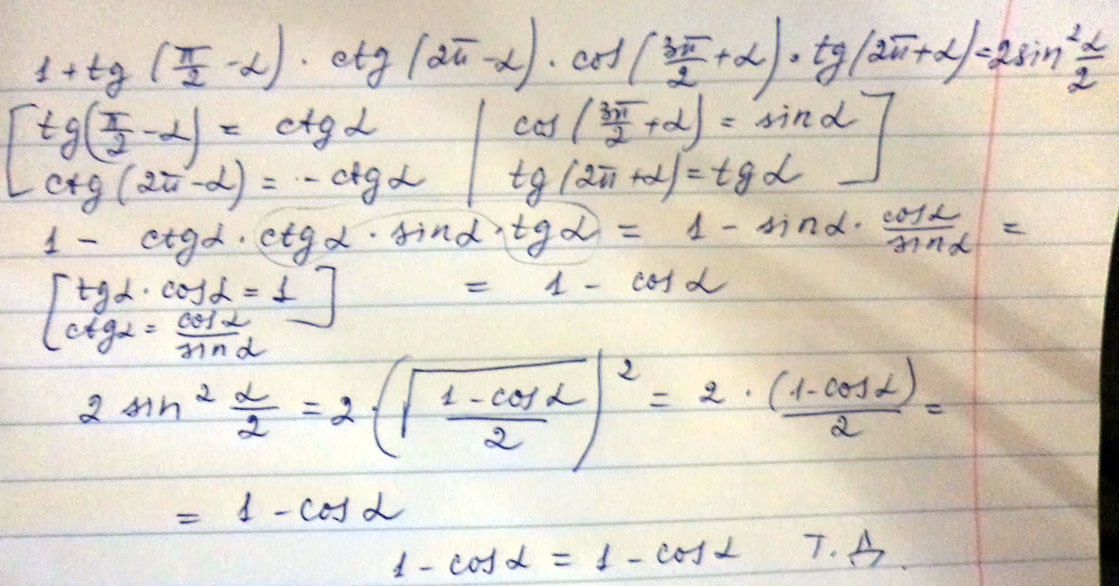тождество »

докажите тождество - страница 15

  • Докажите тождество
    соs2x+tg^2x*cos2x-1=-tg^2x


    Решение: $$ cos(2x)+tg^2(x)*cos(2x)-1=-tg^2(x) \\ cos(2x)++cos(2x)*(\frac{sin(x)}{cos(x)})^2-1=-(\frac{sin(x)}{cos(x)})^2 \\ cos(2x)+\frac{cos(2x)sin^2(x)}{cos^2(x)}=-\frac{sin^2(x)}{cos^2(x)} \\ \frac{cos(2x)sin^2(x)+cos^2(x)cos(2x)-cos^2(x)}{cos^2(x)}=-\frac{sin^2(x)}{cos^2(x)} \\ cos(2x)sin^2(x)+cos^2(x)cos(2x)-cos^2(x)=-sin^2(x) \\ (1-2sin^2x)sin^2x+(1-sin^2x)(1-2sin^2x)-(1-sin^2x)=-sin^2x \\ sin^2x-2sin^4x+1-3sin^2x+2sin^4x+sin^2x-1=-sin^2x \\ -sin^2x=-sin^2x $$

  • 1-cost/1+cost=tg^2t/2
    Докажите тождество


    Решение: $$ \frac{1-cost}{1+cost}= \frac{1-cos(2* \frac{t}{2} )}{1+cos(2* \frac{t}{2} )}= \frac{1-(cos^2( \frac{t}{2} )-sin^2( \frac{t}{2} ))}{1+cos^2( \frac{t}{2} )-sin^2( \frac{t}{2} )}= \\ \\ = \frac{1-cos^2( \frac{t}{2} )+sin^2( \frac{t}{2} )}{1+cos^2( \frac{t}{2} )-sin^2( \frac{t}{2} )}= \frac{sin^2( \frac{t}{2} )+sin^2( \frac{t}{2} )}{cos^2( \frac{t}{2} )+cos^2( \frac{t}{2} )}= \\ \\ = \frac{2sin^2( \frac{t}{2} )}{2cos^2( \frac{t}{2} )}=tg^2( \frac{t}{2} ) \\ \\ \\ \\ tg^2( \frac{t}{2} )=tg^2( \frac{t}{2} ) $$
    Что и требовалось доказать.

  • Докажите тождество 1) ctgα/tgα+1=1/sin²α 2) ctg²α -cos²α=ctg²α*cos²α


    Решение: 1) Преобразуем левую часть

    =cos(a)\sin(a) : sin(a)\cos(a) +1 = cos^{2}(a)\sin^{2}(a) + 1 = (cos^{2}+sin^{2})\sin^{2}(a) = 1\sin^{2)(a)

    Левая часть равна правой. Тождество доказано.

    2) Также преобразуем левую часть.

    =cos^{2}(a)\sin^{2}(a) - cos^{2}(a)= (cos^{2}(a)(1-sin^{2}(a))\sn^{2}(a) = ctg^{2}(a) * cos^{2}(a)

    Левая часть равна правой. Тождество доказано.

  • Докажите тождество 1+tg (П/2-a)*ctg (2П-a)*cos (3П/2+a)*tg (2П+a)=2sin^2a/2


    Решение:

    1+ctga*(-ctga)*sina*tga=1-cosa/sina *sina=1-cosa
    2sin²(a/2)=1-cosa
    1-cosa=1-cosa

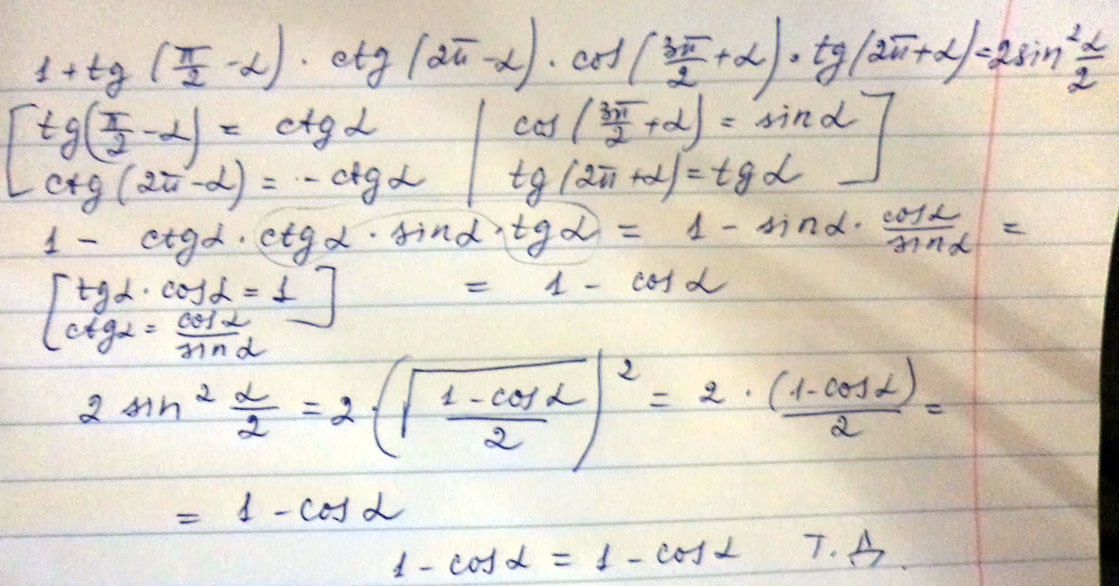
    ctga -ctga sina tga -cosa sina sina -cosa sin a -cosa -cosa -cosa...

  • Упоростите выражение 1- sin2tcost / 2sint Решите уравнение sin5x = sin3x Докажите тождество 2cos^2(45©+4a)+sin8a=1 Вычислите cos70©+sin140© - cos10©


    Решение: 1- sin2tcost / 2sint= 1 -2sintcostcost/2sint=1 -cos^2t=sin^2t

     sin5x = sin3x sin5x -sin3x=0 2sinxcos4x=0

    sinx=0 x=pi n, neZ

    cos4x=0 4x=pi/2+pi k x=pi/8+1/4pi k, keZ

    cos70©+sin140© - cos10©=cos(90-20)+sin(180-40)+cos10=sin20+sin40+cos10=

    =2sin30cos10+cos10=2*1/2*cos10+cos10=2cos10

     2cos^2(45©+4a)+sin8a=1

     2cos^2(45©+4a)-1= -sin8a

    cos2{(45©+4a)}=cos(90+8a)= - sin8a

<< < 131415 16 17 > >>