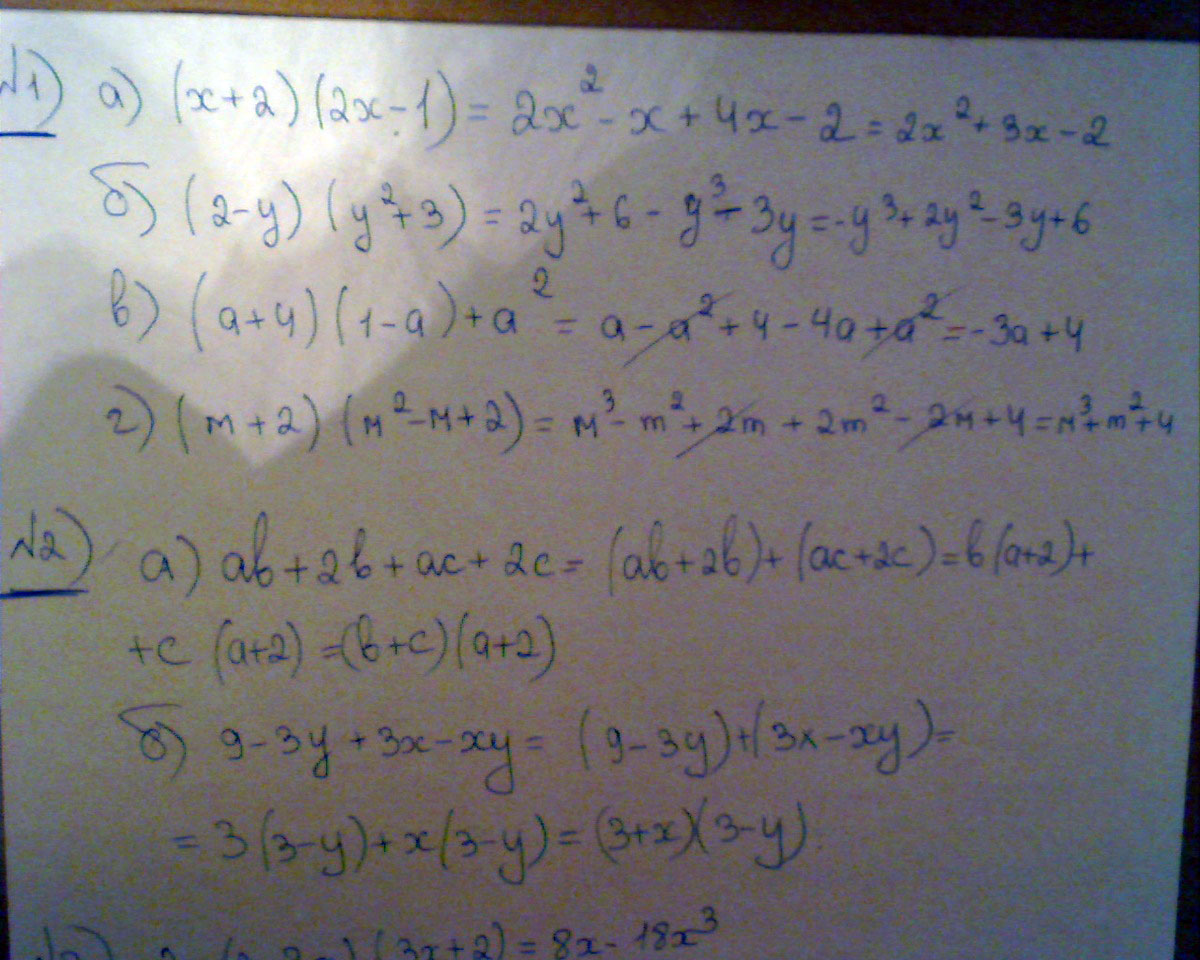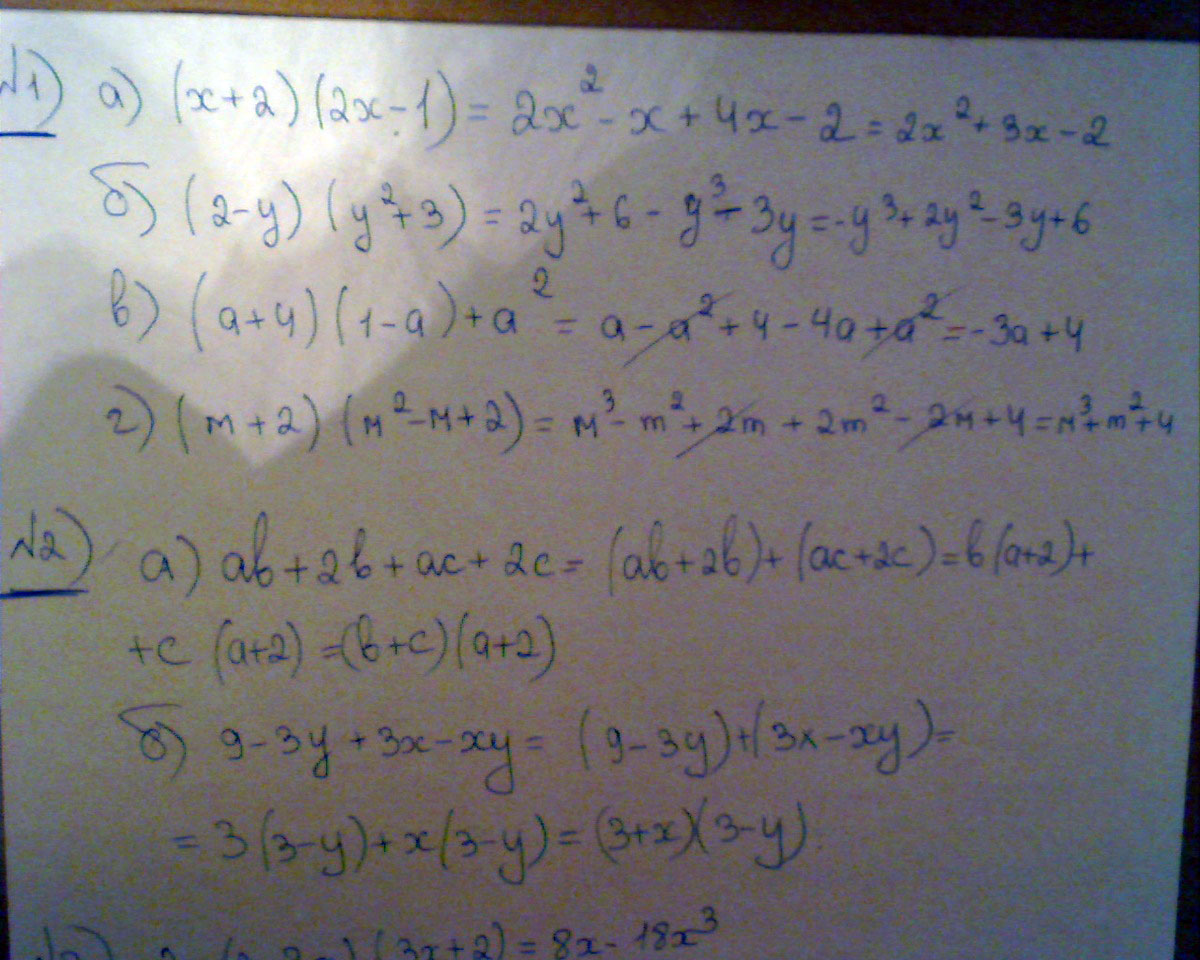докажите тождество - страница 17
докажите тождества:
а)sinx/2*cosx/2= 1/2 sinx
б)cos^2 x/4 - sin^2 x/4= cos x/2
Решение: по формуле синуса двойного угла $$ sin (2 \alpha)=2*sin \alpha* cos \alpha $$:$$ sin \frac{x}{2} *cos \frac{x}{2}=\frac{1}{2}*2sin \frac{x}{2} *cos \frac{x}{2}=\frac{1}{2}*sin(2*\frac{x}{2})=\frac{1}{2}*sin x $$
доказано
по формуле косинуса двойного угла $$ cos (2 \alpha)=cos^2 \alpha -sin^2 \alpha $$:
$$ cos^2 \frac{x}{4}-sin^2 \frac{x}{4}=cos (2*\frac{x}{4})=cos \frac{x}{2} $$
доказано
Докажите тождества:
a) cos^2 альфа + tg^2 альфа + sin^2 альфа = tg^2 альфа +1
б) sin^2 альфа - cos^2 альфа +1 = 2 sin^ альфа
в) (sin альфа +1) (sin альфа -1) = -cos^2 альфа
г) tg альфа + ctg альфа = 1\cos альфа * sin альфа
Решение: А)cos^2α+sin^2α=1
cos^2α+sin^2α+tq^2α=1+tq^2α
б) 1-cos^α=sin^2α
sin^2α-cos^2α+1=sin^2α+sin^2α=2sin^2α
в)(sinα+1)(sinα-1)=sin^2α-1^2=sin^2α-1= - cos^2α
г)tqα+ctqα=(sinα/cosα)+(cosα/sinα)=(sin^2α+cos^2α)/(sinα*cosα)=1/(sinα*cosα)А) cos²α+tg²α+sin²α=tg²α+1
(cos²α+sin²α)+tg²α=tg²α+1
1+tg²α=tg²α+1 тождество доказано
б) sin²α-cos²α+1=2sin²α
sin²α+(1-cos²α)=2sin²α
sin²α+sin²α=2sin²α
2sin²α=2sin²α
в)(sinα+1)(sinα-1)=-cos²α
sin²α-1=-cos²α
-(1-sin²α)=-cos²α
-cos²α=cos²α
г) tgα+ctgα=1/(cosα×sinα)
sinα/cosα+cos/sin=1/(cosα×sinα)
(sin²α+cos²α)/sinαcosα=1/(cosα×sinα)
1/(sinαcosα)=1/(cosα×sinα)докажите тождества а)cos в квадрате альфа + tg в квадрате альфа + sin в квадрате альфа =tg в квадрате альфа +1 б)sin в квадрате альфа - cos в квадрате альфа + 1 =2 sin в квадрате альфа в) (sin альфа +1) (sin альфа -1 )= - cos в квадрате альфа.
Решение: а)cos в квадрате альфа + sin в квадрате альфа равно 1 это главное тригонометрическое тождествои получится tg в квадрате альфа + 1=tg в квадрате альфа + 1
б)sin в квадрате альфа-cos в квадрате альфа+cos в квадрате альфа + sin в квадрате альфа=2sin в квадрате альфа
2sin в квадрате альфа=2sin в квадрате альфа
в) перемножаем и получается sin в квадрате альфа-1=-cos в квадрате альфа
и получается sin в квадрате альфа-sin в квадрате альфа-cos в квадрате альфа=cos в квадрате альфа
cos в квадрате альфа=cos в квадрате альфа
Докажите тождество: ах-у+х-ау=(х-у)(а+1)
Решение: Ax + x - ay - y
Я переписала в удобный вид, при котором видно, что надо вынести за скобки
Мы выноси в первой группе(ax + x) х, а во второй у
Получаем: x(a + 1) - y(a + 1)
У нас появляется общий множитель - a + 1
Выносим его за скобку, получаем: (а + 1)(х - у)
Тождество доказаноАх - ау +х -у = а(х-у) +(х-у) = (х-у)(а+1)
1) Упростите выражения а)(х+2)(2х-1)= б) ( 2-у)(у в квадрате+3) в)(а+4)(1-а)+а в квадрате г)(м+2)(м в квадрате - м +2)\ 2) Разложить на множители: а) аб+2б+ас+2с б)9-3у+3х-ху 3) Докажите тождество: 2х(2-3х)(3х+2)=8х-18х в кубе 4) Представьте в виде произведения: а) 2х в кубе + х в квадрате-2х-1 б) 4 аб - б в кубе - 8а в квадрате+2 аб в квадрате 5) ЗАДАЧА: Квадрат задуманного числа на 16 больше, чем произведение двух чисел, меньших задуманного на 1 и на 2 соответственно. Найдите задуманное число.
Решение: а) (х+2) (2х-1)= (х+2) (1х) = х+2х= 3хЗадача номер 5.
х^2=(x-1)(x-2)+16
x^2=x^2-2x-x+2+16
x^2-x^2+2x+x=2+16
3х=18
х=18/3
х=6
Ответ: 6