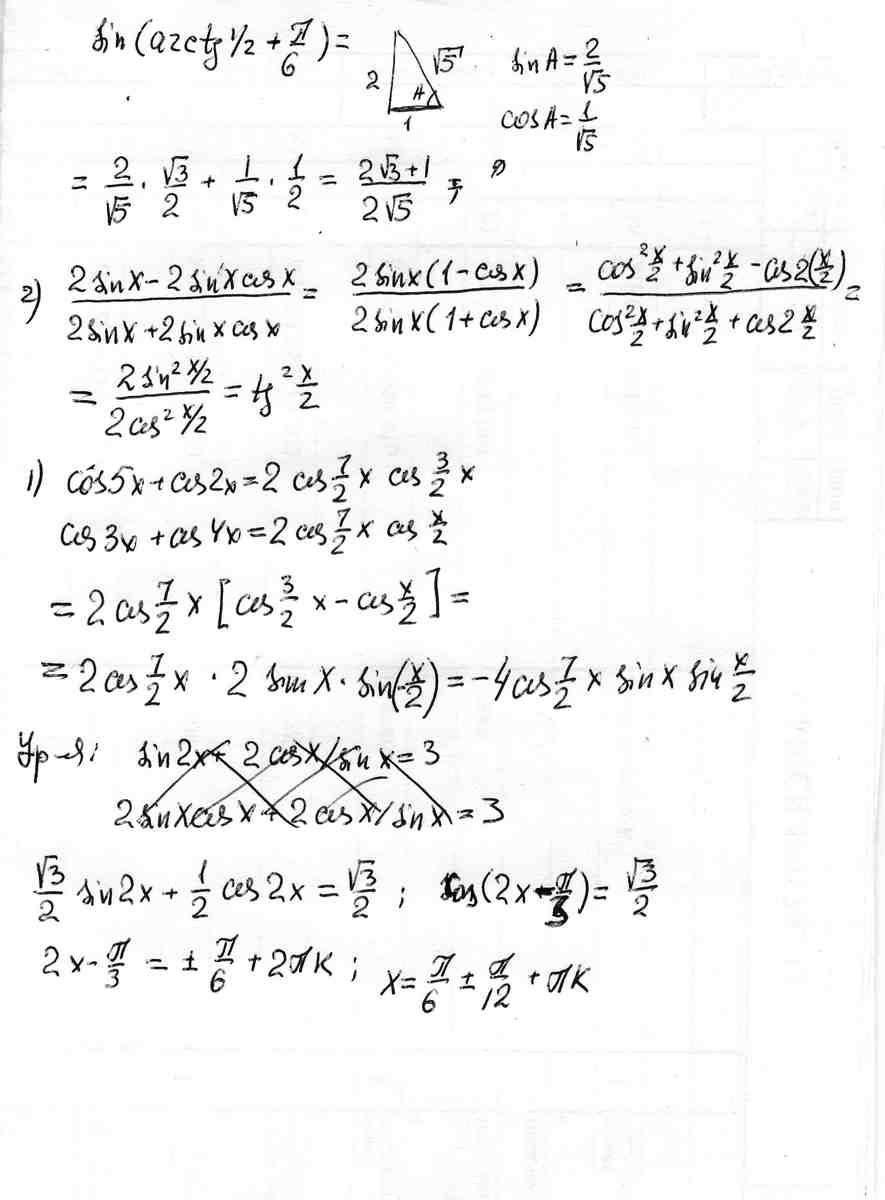тождество »

докажите тождество - страница 12

  • 1) Разложите на множители: а)sin 2a + sin 3a, б) sin 3a - sin a, в) cos x - cos 3x, г) cos 3x - cos 2x

    2) Докажите тождества: а) sin a + sin 5a дробная черта cos a + cos 5a равно tg 3a,

    б) sin 2a + sin 6a дробная черта cos 2a + cos 6a равно tg 4a.


    Решение: 1)sin2a+sin3a=0
    sin5a=0
    5a=pin, принад z
    a=pin/5, принад z
    2)sin3a-sina=0
    sin2a=0
    2a=pin, принад z
    a=pin/2, принад z
    3)cosx-cos3x=0
    cos3x-cosx=0
    cos2x=0
    2x=pi/2+pin, принад z
    x=pi/4+pin/2, принад z
    4)cos3x-cos2x=0
    cosx=0
    x=pi/2+pin, принад z
    1)(sin6a/cos6a)=tg3a
    tg6a=tg3a, тождество не верно,
    2)(sin8a/cos8a)=tg4a
    tg8a=tg4a тождество не верно

  • Докажите тождества cos^2a+tg^2a+sin^2a=tg^2a+1

    sin^2a - cos^2a + 1 =2 sin^2a


    Решение: tg(2*a) * (1-(tg(a))^2)/(1+(tg(a))^2) = sin(2*a); tg(2*a) *((cos(a))^2-(sin(a))^2)/((cos(a))^2+(sin(a))^2)=tg(2*a) *((cos(a))^2-(sin(a))^2)=tg(2*a)*cos(2*a)=sin(2*a)

    cos^2a+tg^2a+sin^2a= cos^2a+sin^2a+tg^2a= tg^2a+1 т. к. основное тригонометрическое тождество гласит cos^2a+sin^2=1

    sin^2a - cos^2a + 1 представим 1 в виде основного тригонометрического тождества, получим. sin^2a - cos^2a+cos^2a+sin^2=sin^2+sin^2=2 sin^2a

  • Докажите тождества:

    1)cos 2x - cos 3x - cos 4x + cos 5x = (-4 sin x/2)*(cos 7x/2)*sin x

    2) (2sinx - sin2x) / (2sinx + sin2x) = tg ^2 (x/2)

    Вычислите:

    sin ( arcctg 1/2 - arcctg( корень из -3))
    Решите уравнения:

    1) корень из (1 -2 sin4x)= -корень из(6) cos2x

    2) корень из (3) sin 2x + cos 2x= корень из (3)

    3)sin 2x+ 2 ctg x=3


    Решение: sin2x+2cosx/sinx=1+2

    2(cosx-sinx)/sinx=(cosx-sinx)^2

    (cosx-sinx)(cosx-sinx-2/sinx)=0

    x=П/4+Пk

    cosx-sinx-2/sinx=0

    cosx*sinx-sin^2(x)=2

    1>sin^2x>0

    cosx*sinx>2, но |sinx|<=1  |cosx|<=1

    следовательно решений уравнение не имеет

    ответ

    x=П/4+Пk

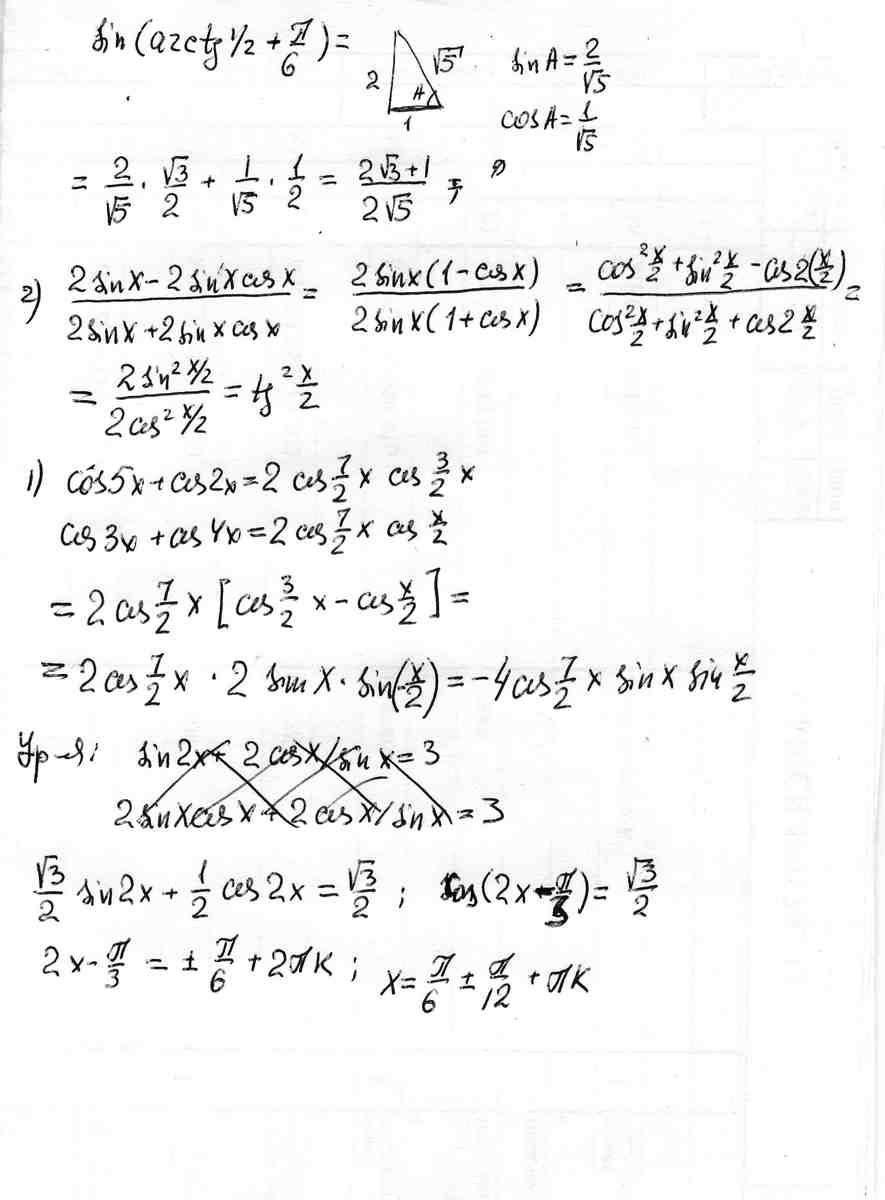
    sin x cosx sinx cosx-sinx sinx cosx-sinx cosx-sinx cosx-sinx- sinx x П Пk cosx-sinx- sinx cosx sinx-sin x sin x cosx sinx но sinx...

  • Докажите тождество:(1-cos2x)/(1+〖cos〗^2 x)=〖tg〗^2 x.


    Решение: A) пользуемся формулой двойного угла)cos2x=cos(квадрат)x-sin(квадрат)x1-(cos(квадрат)x-sin(квадрат)x)\1+ cos(квадрат)x-sin(квадрат)x==1-cos(квадрат)x+sin(квадрат)x\1+ cos(квадрат)x-sin(квадрат)x=основное тригонометрическое тождество cos(квадрат)x+sin(квадрат)x=1следовательно 1-cos(квадрат)x= sin(квадрат)x  2sin(квадрат)x\2cos(квадрат)x двойки сокращаем и получается tg(квадрат)xб) а тут как-то слишком жестоко ))

  • Докажите тождество:
    1-cos2t+sin2t/1+sin2t+cos2t=tg(пи/4-t)


    Решение: (1 + cos2t - sin2t)/(1 + sin2t + cos2t) = (cos^2(t) + sin^2(t) + cos^2(t) - sin^2(t) - 2sintcost)/(cos^2(t) + sin^2(t) + 2sintcost + cos^2(t) - sin^2(t)) = (2cos^2(t) - 2sintcost)/(2cos^2(t) + 2sintcost) = (cos^2(t) - sintcost)/(cos^2(t) + sintcost) = (cost - sint)/(cost + sint)
    по формуле
    bcosx + asinx = sqrt(a^2 + b^2)sin(x + w)
    sinw = b/sqrt(a^2 + b^2); cosw = a/sqrt(a^2 + b^2)
    (cost - sint)/(cost + sint) = (sqrt(2)sin(t + 3П/4))/(sqrt(2)sin(t + П/4) = sin(t + 3П/4)/sin(t + П/4) = sin(П - (П/4 - t))/sin(П/2 - (П/4 - t)) = sin(П/4 - t)/cos(П/4 - t) = tg(П/4 - t)
    чтд

<< < 101112 13 14 > >>