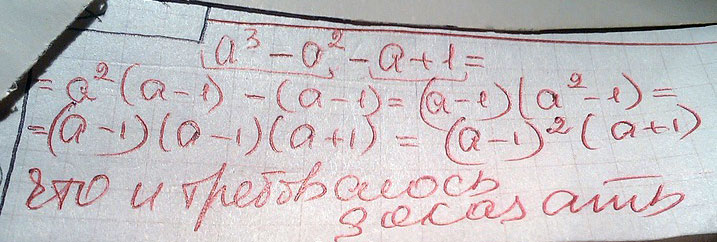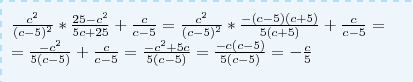тождество »
докажите тождество - страница 21
Докажите тождество. 2 * ( C - 3 )² - 4*( 1 - C )*( C + 1 ) = 6 *( C - 1 )² + 8
3 * ( M - 4)*( 4 + M ) - 3*( 2 - M)² = 12 * ( M - 5 )
Решение: 2 * ( C - 3 )² - 4*( 1 - C )*( C + 1 ) = 6 *( C - 1 )² + 8
2 *( C² - 6C + 9 ) - 4 * ( 1 - C ² ) = 6 * ( C² - 2C + 1 ) + 8
2C² - 12C + 18 - 4 + 4C² = 6C² - 12C + 6 + 8
6C² - 12C + 14 = 6C² - 12C + 14
правая часть равна левой части, что и требовалось доказать
-
3 * ( M - 4)*( 4 + M ) - 3*( 2 - M)² = 12 * ( M - 5 )
3 * ( M² - 16 ) - 3 * ( 4 - 4M + M² ) = 12M - 60
3M² - 48 - 12 + 12M - 3M² = 12M - 60
12M - 60 = 12M - 60
правая часть равна левой части, что и требовалось доказать
Докажите тождество:
a³-a²-a+1=(a-1)²(a+1)
Решение: Раскроем скобки в правой части:
$$ a^3-a^2-a+1=(a^2-2a+1)(a+1) \\ a^3-a^2-a+1=a^3-2a^2+a+a^2-2a+1 \\ a^3-a^2-a+1=a^3-a^2-a+1 $$
что и требовалось доказать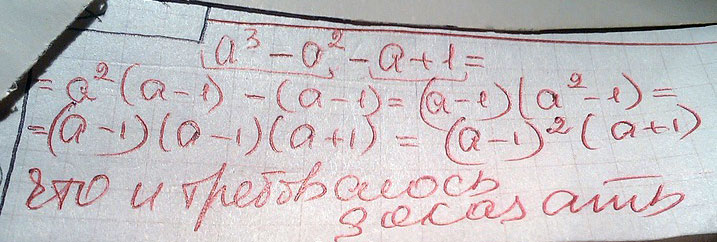
Докажите тождество \(\frac{b}{a-b}-\frac{a^2 - b^2}{a+3b}\cdot(\frac{a+b}{(a-b)^2}+\frac{b}{a^2 - b^2}) = -1 \)
Решение: $$ 1.\;\frac{a+b}{(a-b)^2}+\frac b{a^2-b^2}=\\=\frac{a+b}{(a-b)^2}+\frac b{(a+b)(a-b)}=\\=\frac{(a+b)(a+b)+b(a-b)}{(a-b)^2(a+b)}=\\=\frac{a^2+2ab+b^2+ab-b^2}{(a-b)^2(a+b)}=\frac{a^2+3ab}{(a-b)^2(a+b)}=\frac{a(a+3b)}{(a-b)^2(a+b)}\\2.\;\frac{a^2-b^2}{a+3b}\cdot\left(\frac{a+b}{(a-b)^2}+\frac b{a^2-b^2}\right)=\\=\frac{(a-b)(a+b)}{a+3b}\cdot\frac{a(a+3b)}{(a-b)^2(a+b)}=\\=\frac a{a-b} \\ 3.\;\frac b{a-b}-\frac{a^2-b^2}{a+3b}\cdot\left(\frac{a+b}{(a-b)^2}+\frac b{a^2-b^2}\right)=\\=\frac b{a-b}-\frac a{a-b}=\frac{b-a}{a-b}=\\=\frac{-(a-b)}{a-b}=-1 $$
Ч. Т. Д.Докажите тождество с во втрой/(с-5) во второй * 25-с во втрой/5с+25 +с/с-5=-с/5
Решение: $$ \frac{c^2}{(c-5)^2}* \frac{25-c^2}{5c+25}+ \frac{c}{c-5}= \frac{c^2}{(c-5)^2}* \frac{-(c-5)(c+5)}{5(c+5)}+ \frac{c}{c-5}= \\ =\frac{-c^2}{5(c-5)}+ \frac{c}{c-5}= \frac{-c^2+5c}{5(c-5)}= \frac{-c(c-5)}{5(c-5)}=- \frac{c}{5} $$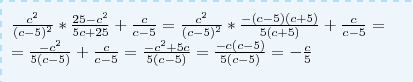
докажите тождество 1/(y-1)(y-2) + 1/(y-2)(y-3) + 1/(y-3)(y-4) = 3/(y-1)(y-4)
Решение: 1/((y-1)(y-2)) + 1/((y-2)(y-3)) + 1/((y-3)(y-4)) = 3/((y-1)(y-4)),1/((y-1)(y-2)) + 1/((y-2)(y-3)) + 1/((y-3)(y-4)) =
= ((y-3)(y-4)+(y-1)(y-4)+(y-1)(y-2))/((y-1)(y-2)(y-3)(y-4)) =
= ((y-4)(y-3+y-1)+(y-1)(y-2))/((y-1)(y-2)(y-3)(y-4)) =
= ((y-4)(2y-4)+(y-1)(y-2))/((y-1)(y-2)(y-3)(y-4)) =
= (2(y-4)(y-2)+(y-1)(y-2))/((y-1)(y-2)(y-3)(y-4)) =
= (y-2)(2(y-4)+y-1)/((y-1)(y-2)(y-3)(y-4)) =
= (2y-8+y-1)/((y-1)(y-3)(y-4)) =
= (3y-9)/((y-1)(y-3)(y-4)) =
= 3(y-3)/((y-1)(y-3)(y-4)) =
= 3 /((y-1)(y-4))