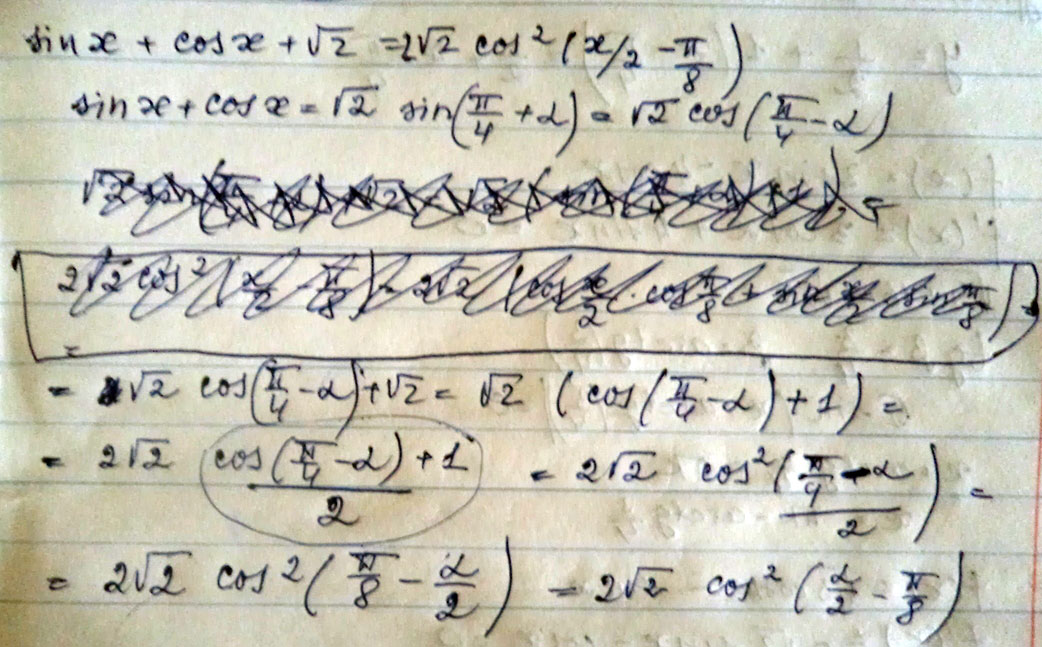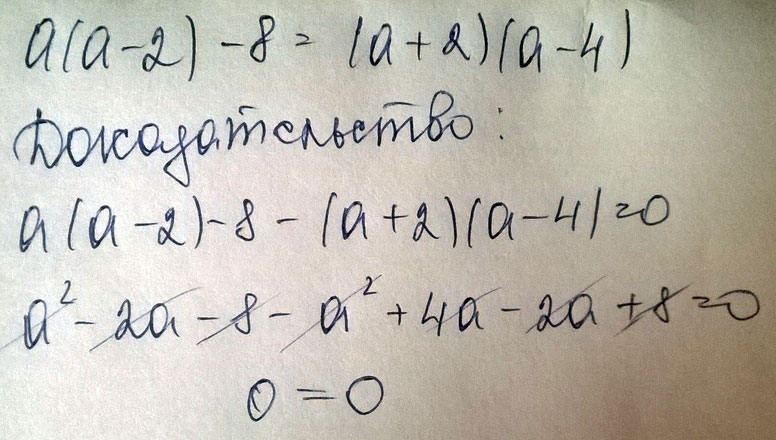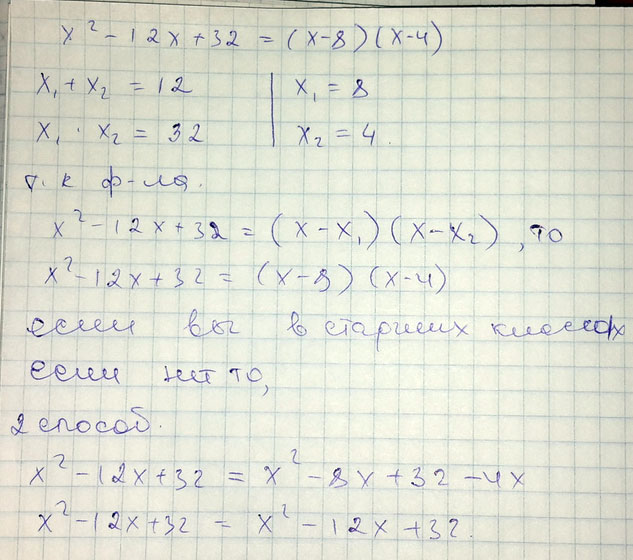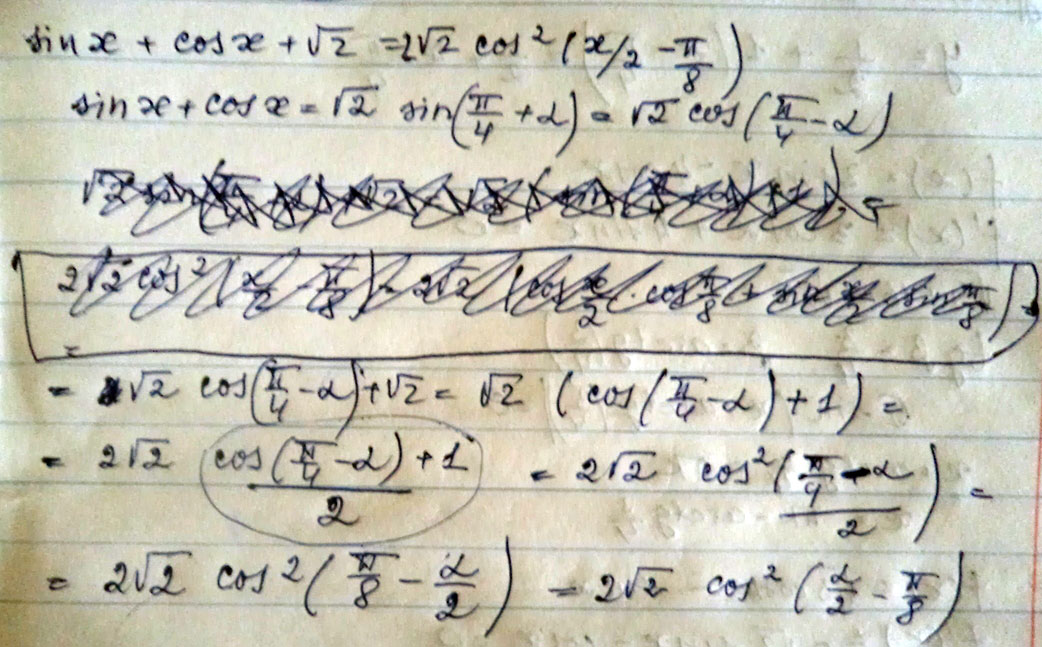тождество »
докажите тождество - страница 25
Докажите тождество a(a-2)-8=(a+2)(a-4)
Решение: Если тождество верно, то при перенесении правой части в левую будет 0
Раскроем скобки в левой части и получится:
а^2-2a-8=(a+2)(a-4)
в левой части получилось квадратное уравнение решаем его:
D= 4+32=36
a1=2-6/2= -2
a2= 2+6/2 = 4
по формуле разложения на множители получается:
(a+2)(a-4)=(a+2)(a-4)
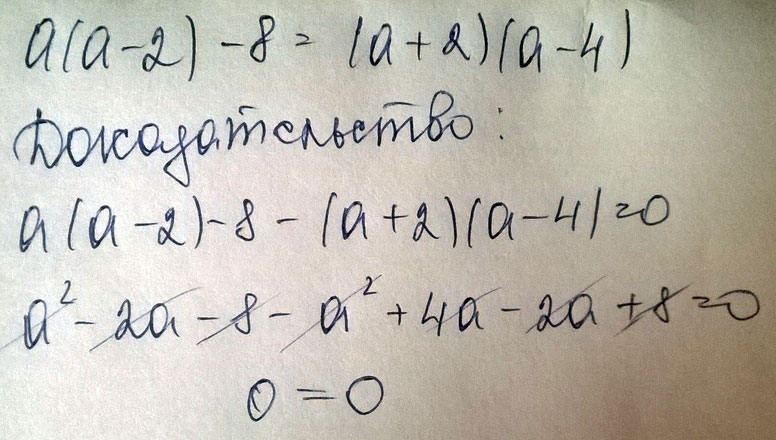
Докажите тождество x^2 - 12x + 32 = (x - 8)(x - 4)
Решение: x^2 - 12x + 32 = (x - 8)(x - 4)
x^2 - 12x + 32 = x^2 - 8x - 4x + 32
x^2 - 12x + 32 = x^2 - 12x + 32
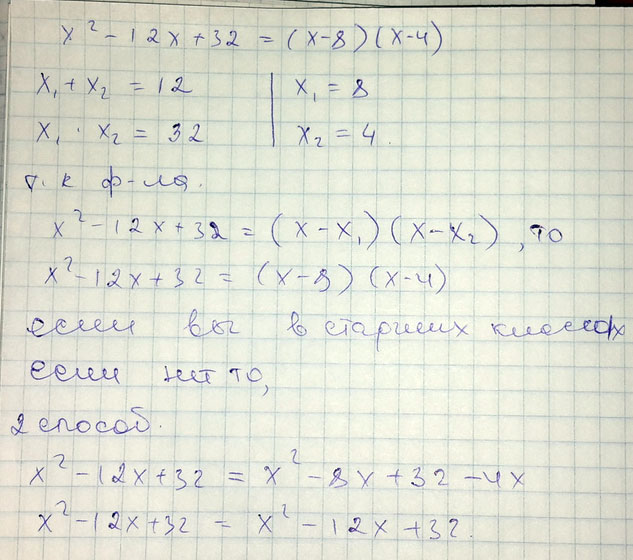
Докажите тождество \( \frac{1+2cos x +cos2x}{1+cos2x-2cosx}=-ctg^2\frac{x}{2} \)
Решение: 1 + 2cos x + cos 2x = 1 + 2cos x + 2cos^2 x - 1 = 2cos^2 x + 2cos x
1 - 2cos x + cos 2x = 1 - 2cos x + 2cos^2 x - 1 = 2cos^2 x - 2cos x
(1 + 2cos x + cos 2x) / (1 - 2cos x + cos 2x) =
= (1 + 2cos x + 2cos^2 x - 1) / (1 - 2cos x + 2cos^2 x - 1) =
= (2cos^2 x + 2cos x) / (2cos^2 x - 2cos x) = (cos x + 1)/(cos x - 1) =
= - (1 + cos x)/(1 - cos x) = - [1 + 2cos^2(x/2) - 1] / [1 - 1 + 2sin^2(x/2)] =
= - (2cos^2(x/2)) / (2sin^2(x/2)) = - (cos(x/2) / sin(x/2))^2 = -ctg^2 (x/2)
Докажите тождество a(a-2)-8=(a+2)(a-4)
Решение: Преобразуем левую часть, оставив правую без изменения: a^2-2a-8. Разложим квадратный трехчлен на множители, для этого найдем корни трехчлена: а1=4; а2=-2.
Квадратный трехчлен вида ax^2+bx+c=a(x-x1)(x-x2);
значит а^2-2a-8=(а-4)(а+2). У нас получилось, что левая часть равна правой, значит заданные выражения тождественны.Докажите тождество:Sin x + cos x +√2= 2√2cos^2(x/2-п/8)
Решение: Sin x + cos x +√2= 2√2cos^2(x/2-п/8)
2√2cos^2(x/2-п/8)=2√2(1+cos(x-pi/4))/2 = √2(1+cos(x-pi/4))=
=√2+√2cos(x)*cos(pi/4)+√2sin(x)*sin(pi/4)) = √2+√2cos(x)*√2/2+√2sin(x)*√2/2 =
= √2+cos(x)+sin(x) - доказано