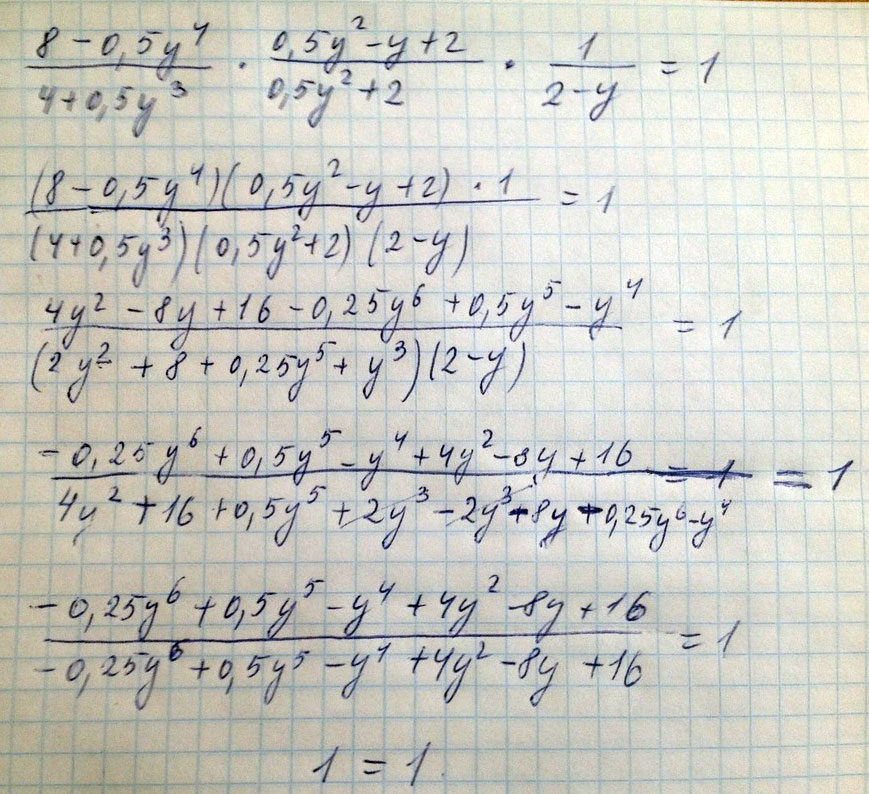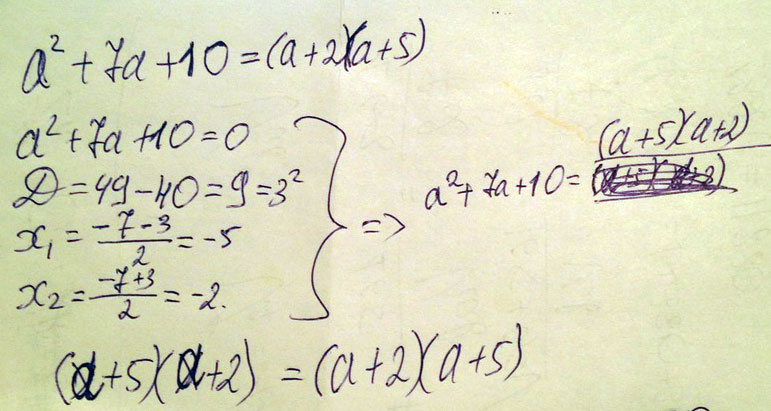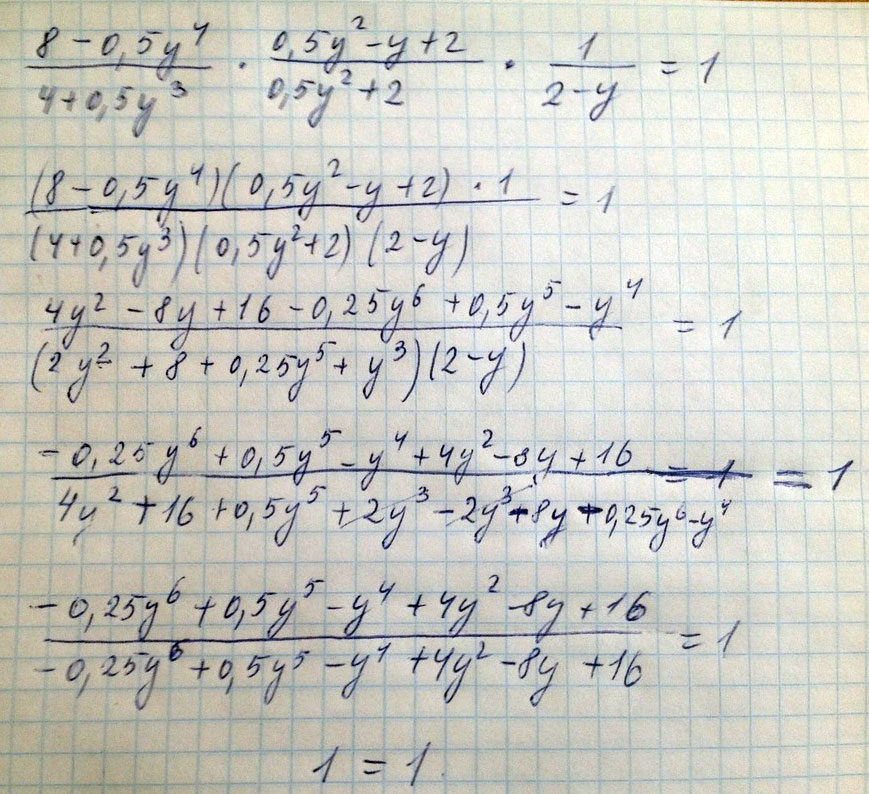докажите тождество - страница 28

докажите тождество (m-n)(2m+3n)(m-7)+7(2m²+2mn-3n²)=m(2m²+mn-3n²+7n)

(2m²+3mn-2mn-3n²)(m-7)+14m²+14mn-21n²=

(2m²+mn-3n²)(m-7)+14m²+14mn-21n²=

2m³-14m²+m²n-7mn-3mn²+21n²+14m²+14mn-21n²=

2m³+m²n-3mn²+7mn=

m(2m²+mn-3n²+7n),

что равняется правой стороне тождества.

(m-n)(2m+3n)(m-7)+7(2m²+2mn-3n²)=

(2m²+3mn-2mn-3n²)(m-7)+14m²+14mn-21n²=

(2m²+(3mn-2mn)-3n²)(m-7)+14m²+14mn-21n²=

(2m²+mn-3n²)(m-7)+14m²+14mn-21n²=

2m³-14m²+m²n-7mn-3mn²+21n²+14m²+14mn-21n²=

2m³+(-14m²+14m²)+m²n-3mn²+(21n²-21n²)+(-7mn+14mn)=

2m³+m²n-3mn²+7mn=

m(2m²+mn-3n²+7n)

что равняется правой стороне тождества (чтд)

Докажите тождество \( \frac{ctg t}{tgt+ctgt}=cos^t \)
Упростите выражение: \( ctgt*sin(-t)+cos(2\pi-t) \)
5. Вычислить: \(2sin870 + \sqrt{12}\cdot cos570 - tg^2 60\)

докажите тождество a во 2 степени +7a+10=(a+2)(a+5)

То, что в левой части приравниваем к 0, т. к. это квадратное уравнение.
Решаем его. А потом по формуле 
а(х-х1)(х-х2), где а-это первые коэф. уравнения(стоит перед х в квадрате)
х1 и х2 - корни уравнения
Получаем (а+5)(а+2)
И это равно (а+2)(а+5)

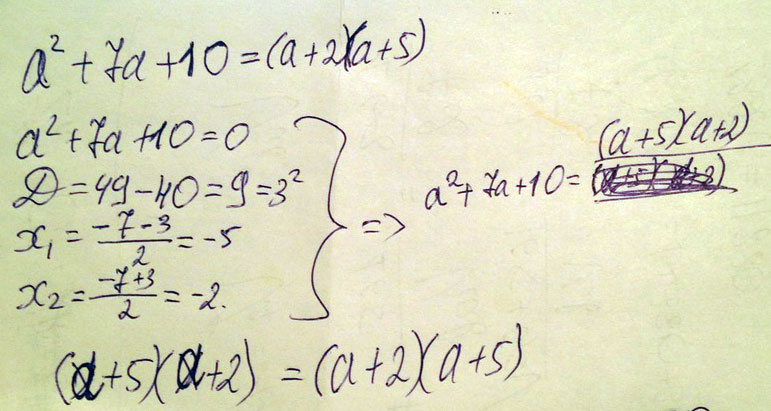
Докажите тождество: \( \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{14}}}}}}=\\=\sqrt[64]{6+\sqrt{35}}+\sqrt[64]{6-\sqrt{35}} \)

Возведем в квадрат обе части уравнения

$$ 2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{14}}}}}=\sqrt[32]{6+\sqrt{35}} \ +2\sqrt[64]{6-\sqrt{35}}\sqrt[64]{6+\sqrt{35}}+\sqrt[32]{6-\sqrt{35}} \\ 2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{14}}}}}= \ \sqrt[32]{6+\sqrt{35}}+2\sqrt[64]{(6-\sqrt{35})(6+\sqrt{35})}+\sqrt[32]{6-\sqrt{35}} \\ 2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{14}}}}} \ =\sqrt[32]{6+\sqrt{35}}+2\sqrt[64]{36-35}+\sqrt[32]{6-\sqrt{35}} \\ 2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{14}}}}}= \ \sqrt[32]{6+\sqrt{35}}+2+\sqrt[32]{6-\sqrt{35}} \\ \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{14}}}}}= \ \sqrt[32]{6+\sqrt{35}}+\sqrt[32]{6-\sqrt{35}} $$

Возведем в квадрат обе части уравнения

$$ 2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{14}}}}= \ \sqrt[16]{6+\sqrt{35}}+2\sqrt[32]{6+\sqrt{35}}\sqrt[32]{6-\sqrt{35}}+\sqrt[16]{6-\sqrt{35}} \\ 2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{14}}}}= \ \sqrt[16]{6+\sqrt{35}}+2+\sqrt[16]{6-\sqrt{35}} \\ \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{14}}}}=\sqrt[16]{6+\sqrt{35}}+\sqrt[16]{6-\sqrt{35}} $$

Возведем в квадрат обе части уравнения

$$ 2+\sqrt{2+\sqrt{2+\sqrt{14}}}= \ \sqrt[8]{6+\sqrt{35}}+2\sqrt[16]{6+\sqrt{35}}\sqrt[16]{6-\sqrt{35}}+\sqrt[8]{6-\sqrt{35}} \\ 2+\sqrt{2+\sqrt{2+\sqrt{14}}}= \ \sqrt[8]{6+\sqrt{35}}+2+\sqrt[8]{6-\sqrt{35}} \\ \sqrt{2+\sqrt{2+\sqrt{14}}}= \ \sqrt[8]{6+\sqrt{35}}+\sqrt[8]{6-\sqrt{35}} $$

Возведем в квадрат обе части уравнения

$$ 2+\sqrt{2+\sqrt{14}}= \ \sqrt[4]{6+\sqrt{35}}+2\sqrt[8]{6+\sqrt{35}}\sqrt[8]{6-\sqrt{35}}+\sqrt[4]{6-\sqrt{35}} \\ \sqrt{2+\sqrt{14}}= \ \sqrt[4]{6+\sqrt{35}}+\sqrt[4]{6-\sqrt{35}} $$

Возведем в квадрат обе части уравнения

$$ 2+\sqrt{14}= \ \sqrt[2]{6+\sqrt{35}}+2\sqrt[4]{6+\sqrt{35}}\sqrt[4]{6-\sqrt{35}}+\sqrt[2]{6-\sqrt{35}} \\ \sqrt{14}= \ \sqrt[2]{6+\sqrt{35}}+\sqrt[2]{6-\sqrt{35}} $$

Возведем в квадрат обе части уравнения

$$ 14= \sqrt[2]{6+\sqrt{35}}+2\sqrt[2]{6+\sqrt{35}}\sqrt[2]{6-\sqrt{35}}+{6-\sqrt{35}} \\ 14= 6+\sqrt{35}+2+6-\sqrt{35} \\ 14=14 $$ => тождество верно

Докажите тождество:

8 - 0,5y^4 0,5y^2-y+2 1

________ × __________ × ___ =1

4+0,5y^3 0,5y^2+2 2-y

(4-y^2)(y^2+4)/ ((y+2) (y^2-2y+4))  (y^2-2y+2) /(y^2+4)  1/(2-y)=

(2-y)(2+y)(y^2+4)/ ((y+2) (y^2-2y+4))  (y^2-2y+2) /(y^2+4)  1/(2-y)=

1