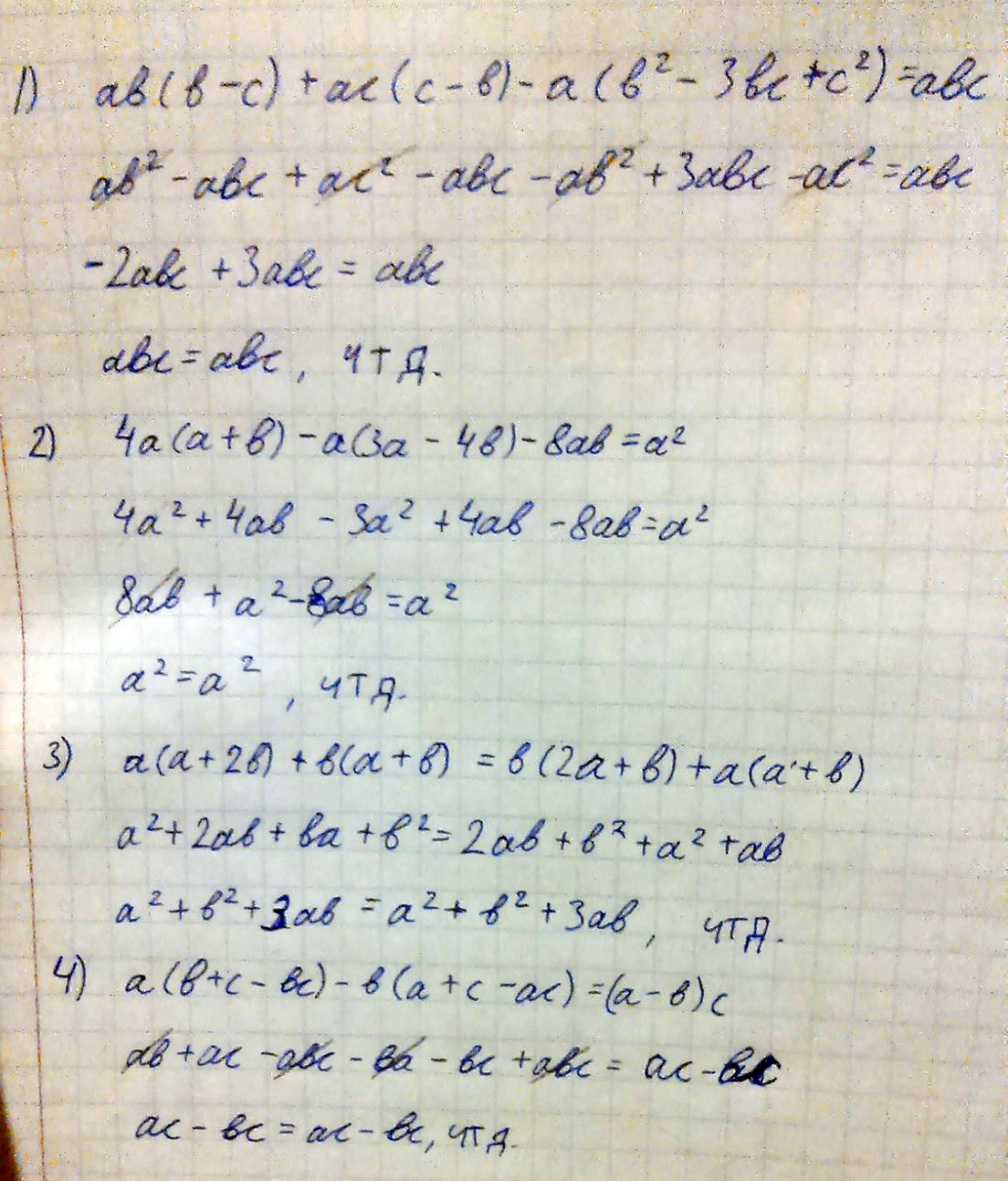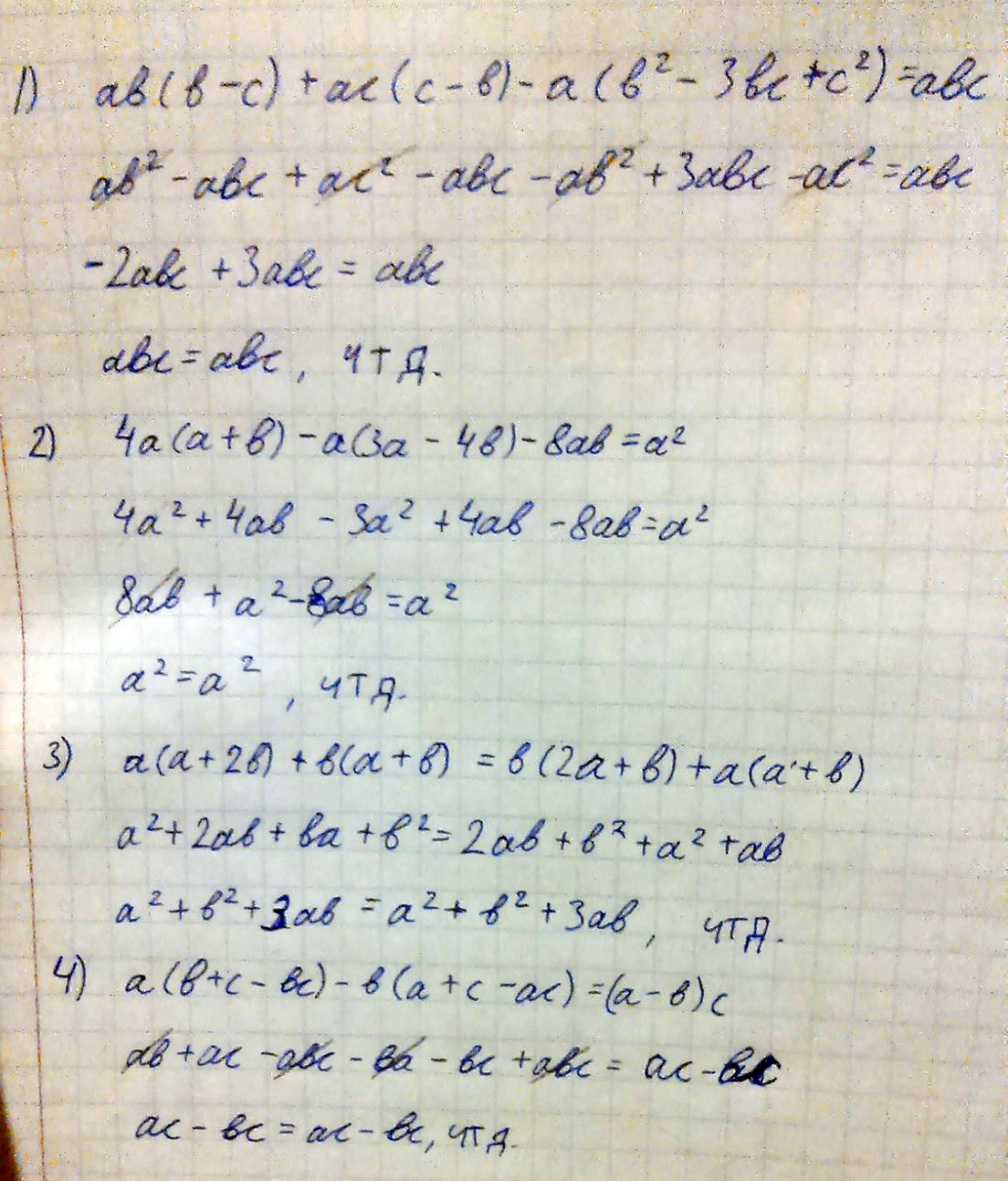докажите тождество - страница 29
докажите тождество y(x+y)^2/x^4-y^4 + x/ x^2+y^2 = 1/ x-y
,
\( y(x+y)^2/(x^4-y^4) + x/ (x^2+y^2) =\\= 1/ (x-y) \)
Решение: Подводим все под общий знаменатель (x^4 - y^4)Числитель: y*(x+y)^2 + x*(x^2 - y^2) - 1*(x+y)*(x^2 + y^2)
Знаменатель: x^4 - y^4
Но теперь можно от знаменателя избавиться, и получится:
y*(x+y)^2 + x*(x^2 - y^2) - 1*(x+y)*(x^2 + y^2) = 0
Раскрываем скобки.
y*(x^2 + 2xy + y^2) + x^3 - xy^2 - 1*(x^3 + xy^2 + x^2y + y^3) = 0
x^2y + 2xy^2 + y^3 + x^3 - xy^2 - x^3 - xy^2 - x^2y - y^3 = 0
0=0
Тождество доказано.
докажите тождество a(b+c)²+b(c+a)²+c(a+b)²-4abc = (a+b)(b+c)(c+a)
Решение: Здесь формулы сокращенного умножения.a(b^2+2bc+c^2)+b(c^2+2ac+a^2)+c(a^2+2ab+b^2)-4abc=
ab^2+2abc+ac^2+bc^2+2abc+ba^2+ca^2+2abc+cb^2-4abc=
ab^2+2abc+ac^2+bc^2+ba^2+ca^2+cb^2=ab^2+2abc+c^2(a+b)+a^2(b+c)+cb^2=
b^2(a+c)+c^2(a+b)+a^2(b+c)+2abc
А (a+b)(b+c)(c+a)= если перемножать первые две скобки, то = ab+ac+b^2+bc и это умножить на третью скобку, то = (c+a)(ab+ac+b^2+bc)= abc+ac^2+b^2c+bc^2+a^2b+a^2c+ab^2+abc=
c^2(a+b)+b^2(c+a)+a^2(b+c)+2abc.
Эти два выражения равны, то есть
b^2(a+c)+c^2(a+b)+a^2(b+c)+2abc = c^2(a+b)+b^2(c+a)+a^2(b+c)+2abc то есть = (a+b)(b+c)(c+a)=(a+b)(b+c)(c+a)
Докажите тождество \(\frac{a^3 -4a}{a+3}\cdot(\frac{3a+9}{2+a} - \frac{2a^2+9a+9}{a^2+4a+4})=\frac{a^2+6a+9}{a^2-4}\cdot \frac{a^3-4a^2+4a}{3+a} \)
Решение: Левая часть
1)(3a+9)/(2+a)-(2a²+9a+9)/(2+a)2=[(3a+9)(2+a)-2a²-9a-9)/(2+a)²=
=(6a+18+3a²+9-2a²-9a-9)/(2+a)²=(a²+6a+9)/(2+a)²=(a+3)²/(2=a)2
2)a(a-2)(a+2)/(a+3)*(a+3)²/(2+a)²=a(a-2)(a+3)/(2+a)
Правая часть
(a+3)²/(a-2)(a+2) * a(a-2)²/(a+3)=a(a-2)(a+3)/(a+2)
a(a-2)(a+3)/(2+a)=a(a-2)(a+3)/(a+2)

Докажите тождество (m+n)*(m^2-mn+n^2)=m^3+n^3
Решение: Просто открываем скобки * * *
(m+n)*(m² - mn+n²) =m³-m²n+mn² +nm² -mn²+n³ = m³+n³.
* * * или обратном порядке * * *
Используем тождество : (m+n)³ =m³+3m²n+3mn²+n³ = m³+n³ +3mn(m+n) ⇒
m³+n³ =(m+n)³ - 3mn(m+n) =(m+n)( ((m+n)² - 3mn) =
(m+n)( (m²+2mn+n² - 3mn) = m+n)( (m² mn+n²).
Докажите тождество: 1) ab(b-c)+ac(c-b)-a(b²-3bc+c²) = abc; 2) 4a(a+b)-a(3a-4b)-8ab = a²; 3) a(a+2b)+b(a+b) = b(2a+b)+a(a+b); 4) a(b+c-bc)-b(a+c-ac) = (a-b)c
Решение: