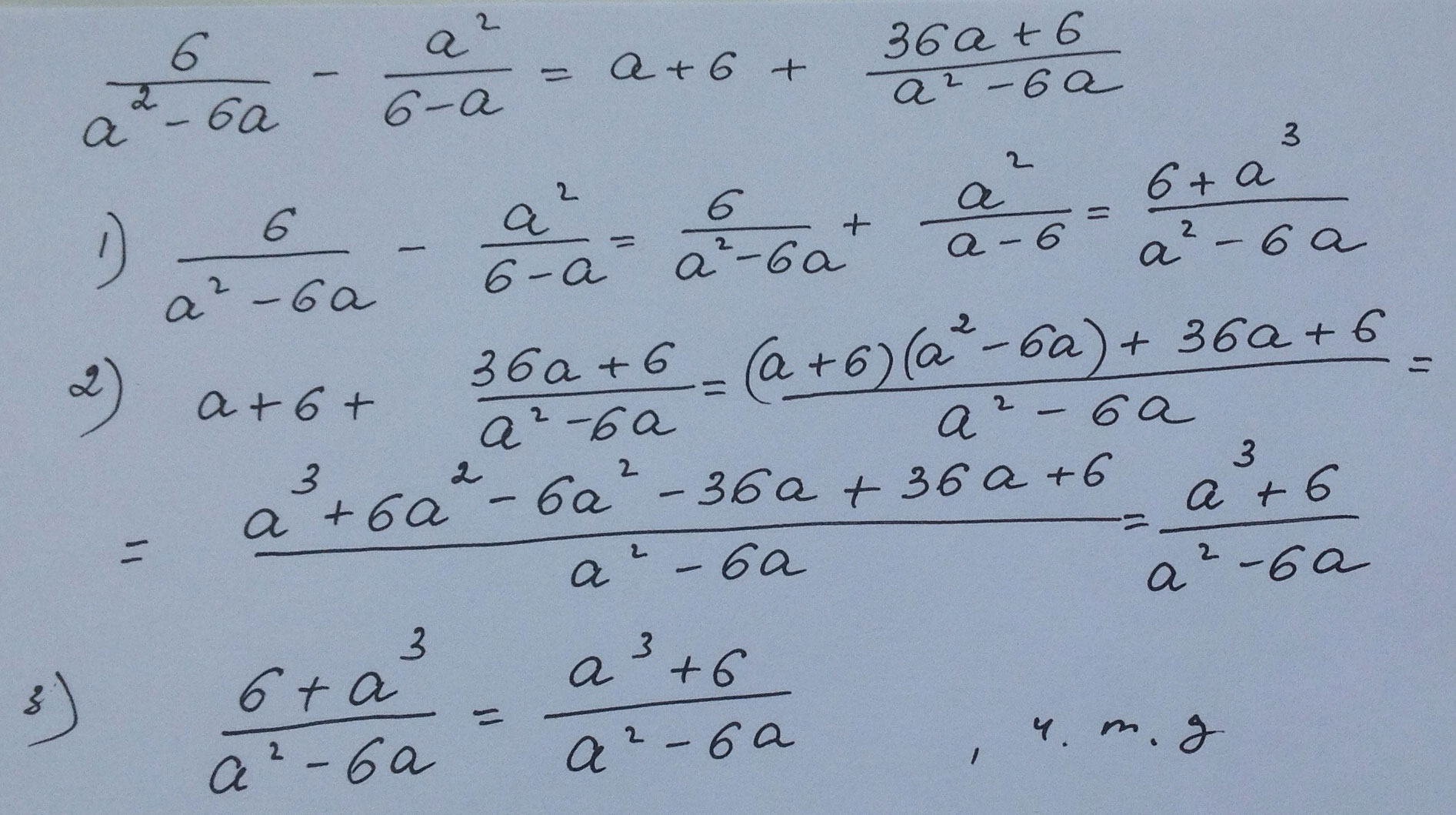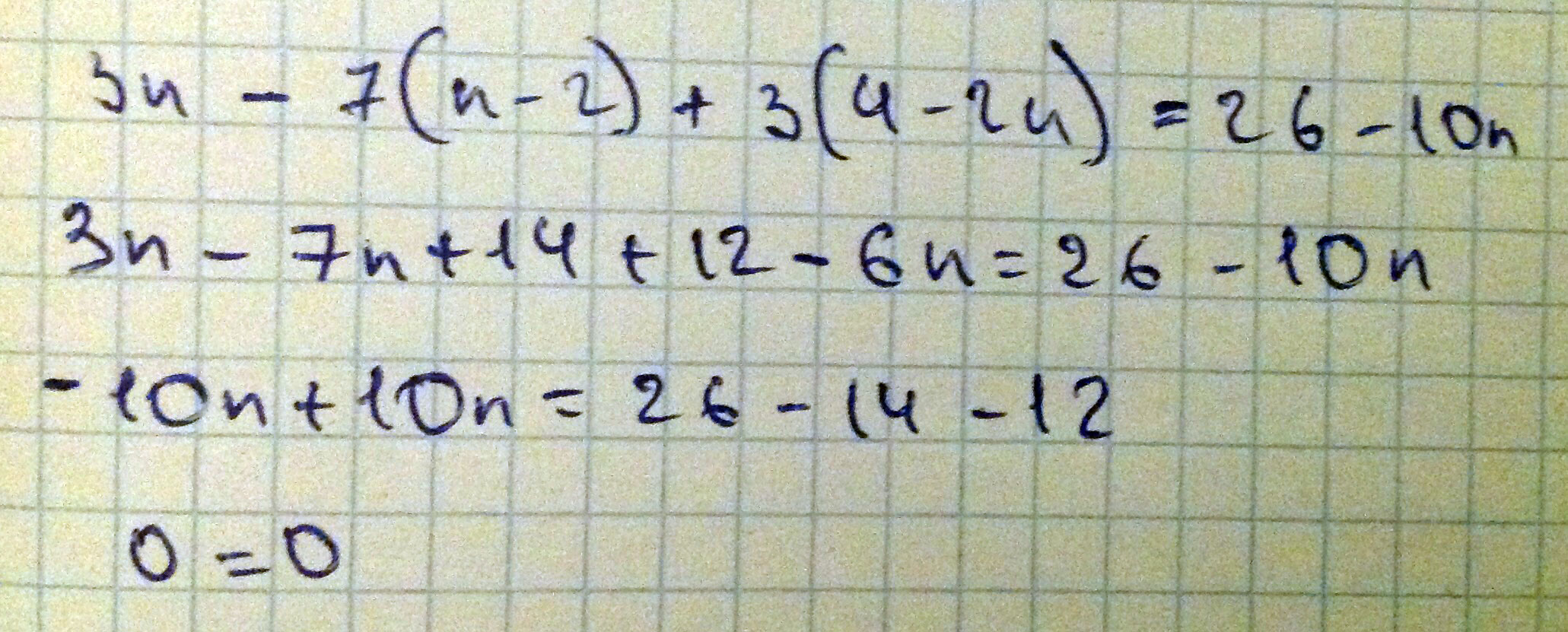тождество »

докажите тождество - страница 32

  • Докажите тождество \( \displaystyle \left(\frac{8y^2+2y}{8y^3-1}-\frac{2y+1}{4y^2+2y+1}\right)\\ \cdot\left(1+ \frac{2y+1}{2y}-\frac{4y^2+10y}{4y^2+2y}\right):\frac{1}{2y}=\frac{2y-1}{2y+1} \)


    Решение: $$ \displaystyle \left(\frac{8y^2+2y}{8y^3-1}-\frac{2y+1}{4y^2+2y+1}\right)\cdot\left(1+ \frac{2y+1}{2y}-\frac{4y^2+10y}{4y^2+2y}\right):\frac{1}{2y}= \\ \\ \left(\frac{8y^2+2y}{(2y-1)(4y^2+2y+1)}-\frac{2y+1}{4y^2+2y+1}\right)\cdot \\ \\ \left(1+ \frac{2y+1}{2y}-\frac{4y^2+10y}{2y(2y+1)}\right):\frac{1}{2y}= \\ \\ \frac{8y^2+2y-(2y+1)(2y-1)}{(2y-1)(4y^2+2y+1)}\cdot \\ \\ \frac{2y(2y+1)+(2y+1)^2-4y^2-10y}{2y(2y+1)}: \frac{1}{2y}= \\ \displaystyle \frac{8y^2+2y-4y^2+1}{(2y-1)(4y^2+2y+1)}\cdot \frac{4y^2+2y+4y^2+4y+1-4y^2-10y}{2y(2y+1)}:\frac{1}{2y}= \\ \\ \frac{4y^2+2y+1}{(2y-1)(4y^2+2y+1)}\cdot \frac{4y^2-4y+1}{2y(2y+1)}: \frac{1}{2y}= \\ \\ \frac{1}{2y-1}\cdot \frac{(2y-1)^2}{2y(2y+1)}\cdot2y= \frac{2y-1}{2y+1} $$

  • Докажите тождество,
    6/a^2-6a -( a^2/6-a=a+6 + (36 a+6/a^2-6a
    (Скобочка означает -начало следующей обыкновенной алгебраической дроби.


    Решение:

    Вычтем из обоих частей 6/(a^2-6)
    Остается:
    a^2/(a-6)=a+6+36/(a-6)
    Домножим все на (а-6)
    Получим
    a^2=(a+6)*(a-6)+36
    Раскрываем скобки справа
    a^2=a^2-36+36
    a^2=a^2
    Тождество справедливо.

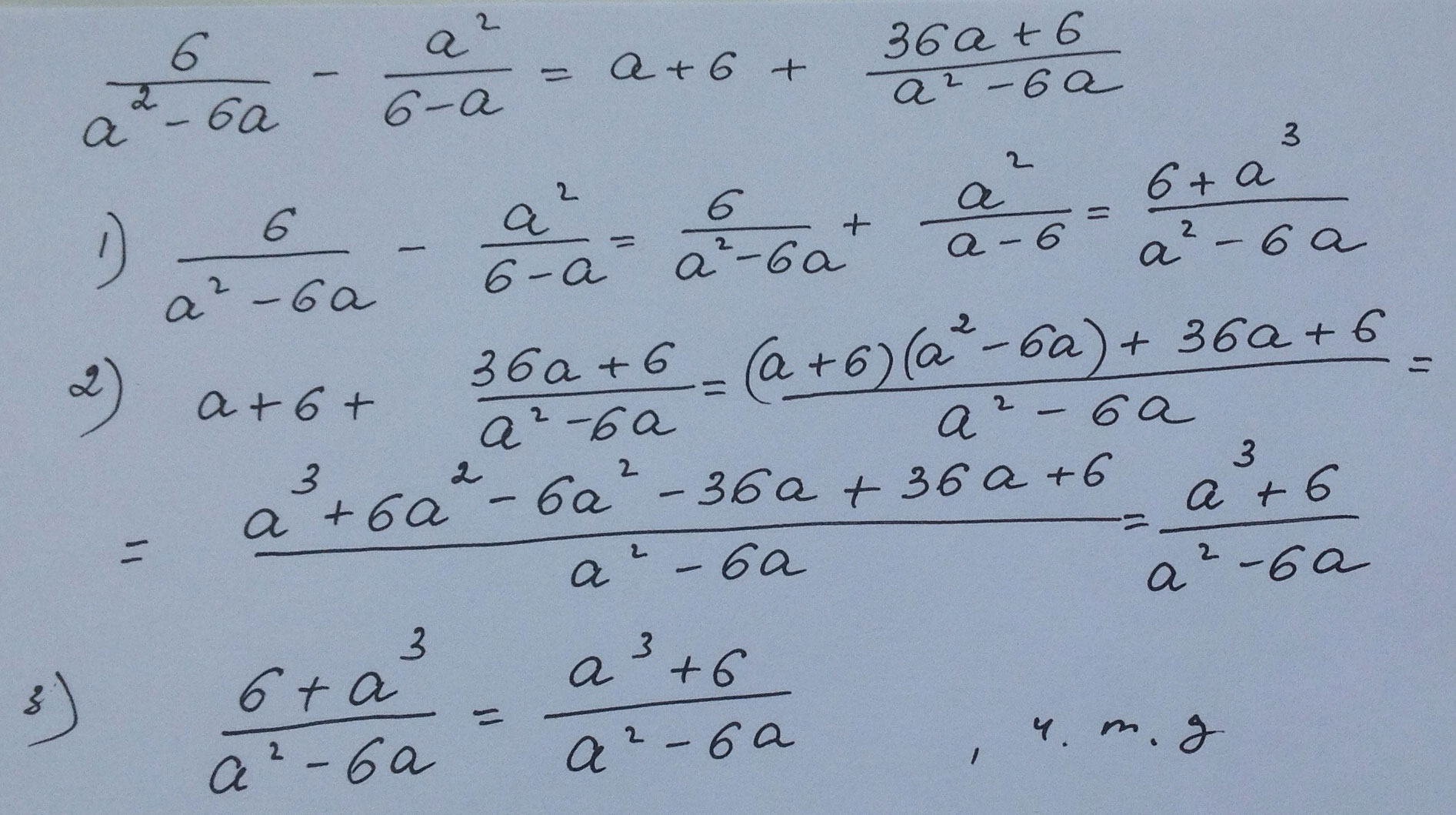
    Вычтем из обоих частей a - Остается a a- a a- Домножим все на а- Получимa a a- Раскрываем скобки справаa a - a a Тождество справедливо....

  • Докажите тождество
    3n-7*(n-2)+3*(4-2n)=26-10n


    Решение: Раскроем скобки

    3n-7n+14+12-6n=26-10n

    3n-7n-6n+10n=26-14-12

    0=0

    Раскрываете скобки, переносите с n в одну сторону, а целые числа в другую, получаем 0=0

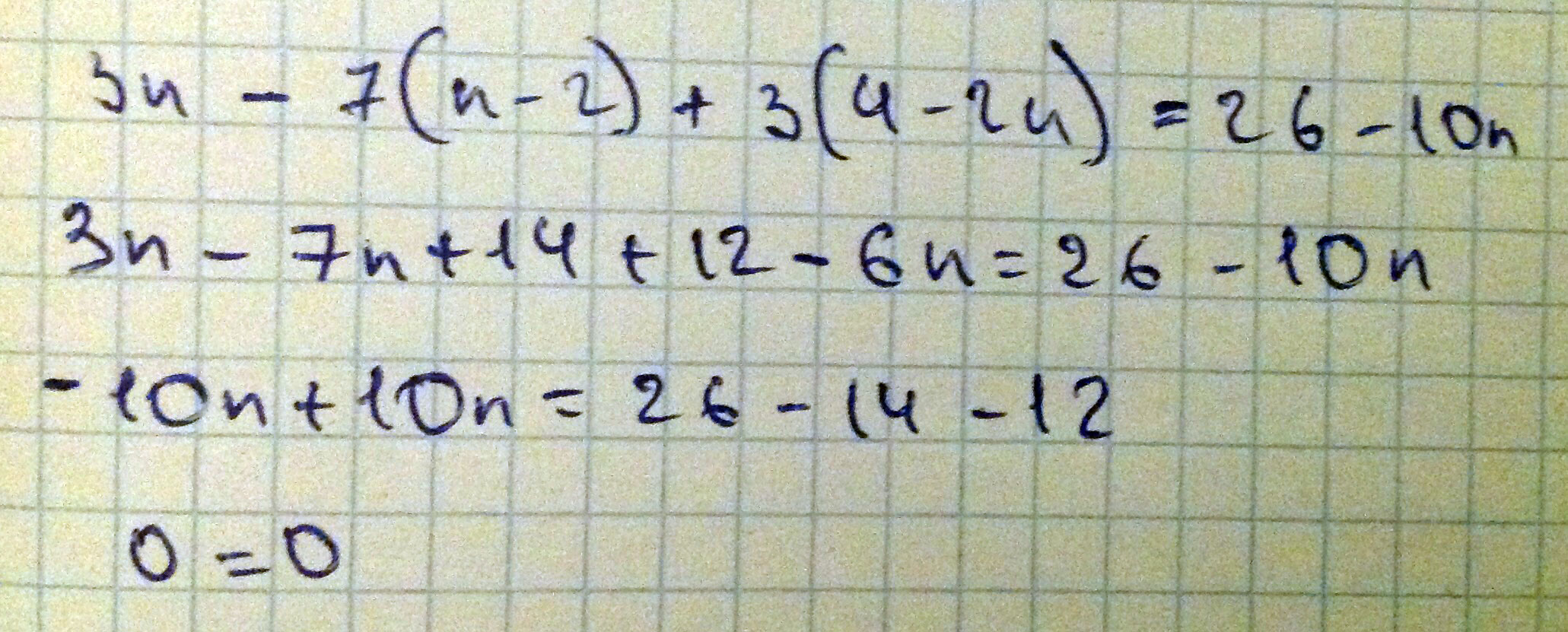
    Раскроем скобки n- n - n - n n- n- n n - - Раскрываете скобки переносите с n в одну сторону а целые числа в другую получаем...

  • Докажите тождество \( \frac{abc-a^3}{a^2b}+\frac{abc-b^3}{b^2c}+\frac{abc-c^3}{c^2a}=0 \)


    Решение: $$ \displaystyle \frac{abc-a^3}{a^2b}+\frac{abc-b^3}{b^2c}+\frac{abc-c^3}{c^2a}= \\ \\ \frac{a(bc-a^2)}{a^2b}+ \frac{b(ac-b^2)}{b^2c}+\frac{c(ab-c^2)}{c^2a}= \\ \\ \frac{bc-a^2}{ab}+\frac{ac-b^2}{bc}+\frac{ab-c^2}{ac}= \\ \\ \frac{c(bc-a^2)+a(ac-b^2)+b(ab-c^2)}{abc} = \\ \\ \frac{bc^2-a^2c+a^2c-ab^2+ab^2-bc^2}{abc} = \frac{0}{abc}=0 $$

  • Докажите тождество а) корень из 7 -4 корнеи из 3=2 - корень из 3 б) корень из 7 +2 корнеи из 10=корень из 5+ корень из 2


    Решение: $$ \sqrt{a^2}=|a|= \left \{ {{a,\; esli\; a \geq 0} \atop {-a,\; \; esli\; a\ < \ 0}} \right. \\\\1)\; \; \sqrt{7-4\sqrt3} = \sqrt{4+3-2\cdot 2\sqrt3} = \sqrt{2^2-2\cdot 2\sqrt3+(\sqrt3)^2} =\\\\= \sqrt{(2-\sqrt3)^2} =|2-\sqrt3|=\{\; (2-\sqrt3)\ > \ 0\; \}=2-\sqrt3\\\\2)\; \; \sqrt{7+2\sqrt{10}} = \sqrt{5+2+2\cdot \sqrt{5\cdot 2}} = \sqrt{(5)^2+2\cdot \sqrt5\cdot \sqrt2+(\sqrt2)^2} =\\\\= \sqrt{(\sqrt5+\sqrt2)^2} =|\sqrt5+\sqrt2|=\{(\sqrt5+\sqrt2)\ > \ 0\}=\sqrt5+\sqrt2 $$

<< < 303132 33 34 > >>