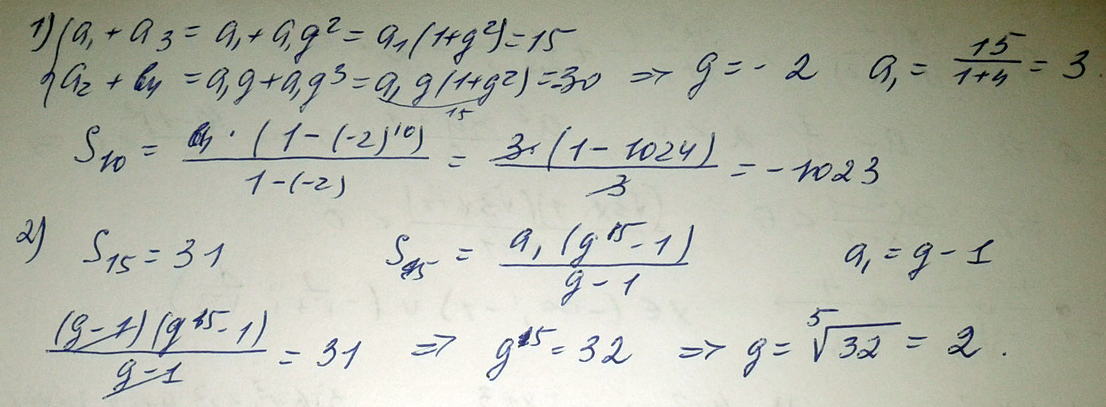прогрессия »
второй член геометрической прогрессии - страница 10
Сумма первого третьего членов возрастающей геометрической прогресса равна 10 а её второй член равен 3 найти произведение первого и пятого членов прогрессии
Решение: Геометрическая прогрессия возрастающая, значит q>1
$$ \left \{ {{b_{1}+b_{3}=10} \atop {b_{2}=3=b_{1}*q}} \right. $$
$$ b_{1}+b_{1}*q^{2}=10 $$
$$ b_{1}*(1+q^{2})=10 $$
$$ b_{1}= \frac{3}{q} $$
$$ \frac{3}{q}*(1+q^{2})=10 $$
$$ \frac{3}{q}+\frac{3q^{2}}{q}=10 $$
$$ \frac{3+3q^{2}-10q}{q}=0 $$
$$ 3q^{2}-10q+3=0, D=100-4*3*3=64=8^{2} $$
$$ q_{1}= \frac{10-8}{6}= \frac{1}{3}<1 $$ - посторонний корень
$$ q_{2}= \frac{10+8}{6}=3\ > \ 1 \\ b_{1}= \frac{3}{q}=\frac{3}{3}=1 $$
$$ b_{1}*b_{5}=b_{1}*b_{1}*q^{4}=b^{2}_{1}*q^{4}=1*3^{4}=81 $$
Ответ: 81
1) Сумма первого и третьего членов геометрической прогрессии равна 15, а сумма второго и четвертого -30. Найдите сумму первых десяти членов прогрессии.
2) Сумма первых пяти членов геометрической прогрессии равна 31. Первый член на единицу меньше знаменателя прогрессии. Найдите знаменатель.
Решение: 1)
b1+b3=b1+b1q²=b1(1+q²)=15
b2+b4=b1q+b1q³=b1q(1+q²)=-30
Поделим одно на другое и получим:
q=-2, b1=3
S10=b1(q^n-1)/(q-1)=3·1023/(-3)=-1023
2)
b1=x
q=x+1
S5=x((x+1)^5-1)/x=(x+1)^5-1=31
(x+1)^5=32
x+1=2⇒x=1⇒q=2.
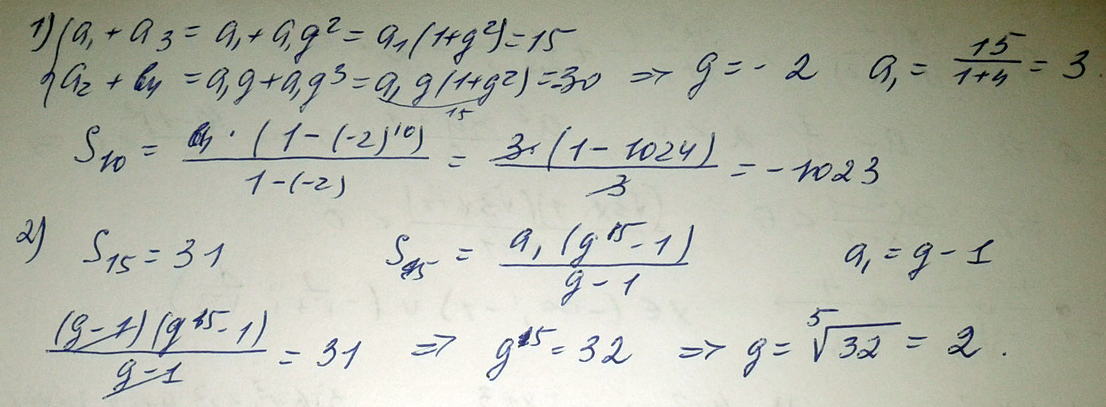
Сумма первого и третьего членов геометрической прогрессии равна 10, а сумма второго и четвертого членов равна 20. Найдите первый член этой прогрессии. Напишите подробное решение
Решение: $$ b_n=b_1\cdot q^{n-1};==>b_2=b_1\cdot q=b_1\cdot q^{2-1}\\ \left \{ {{b_1+b_3=10} \atop {b_2+b_4=20}} \right. \\ b_1-;\\ \left \{ {{b_1+b_1\cdot q^2=10} \atop {b_1\cdot q+b_1\cdot q^3=20}} \right. ;\\ \left \{ {{b_1\cdot(1+q^2)=10;} \atop {b_1\cdot q\cdot(1+q^2)}=20;} \right.\\ \frac{b_1\cdot q\cdot(1+q^2)}{b_1\cdot(1+q^2)}=\frac{20}{10};\\ q=2;\\ b_1+b_1\cdot2^2=10;\\ b_1\cdot(1+4)=10;\\ $$
$$ b_1\cdot5=10;\\ b_1=\frac{10}5=2;\\ b_1\cdot2+\b_2\cdot2^3=20;\\ b_1\cdot(2+8)=20;\\ b_1\cdot10=20;\\ b_1=\frac{20}{10}=2. $$
первій член прогрессии равен 2
Сумма второй и третий членов геометрической прогрессии равна 30, и разница четвертого и второй равна 90. Найти первый член прогрессии.
Решение: $$ \begin{cases} b_2+b_3=30 \\ b_4-b_2=90 \end{cases} \ < \ =\ > \ \begin{cases} b_2+b_2q=30 \\ b_2q^2-b_2=90 \end{cases} \ < \ =\ > \ \begin{cases} b_2(q+1)=30 \\ b_2(q^2-1)=90 \end{cases} \\ \begin{cases} b_2(q+1)=30 \\ b_2(q-1)(q+1)=90 \end{cases} \ < \ =\ > \ \begin{cases} b_2(q+1)=30 \\ 30(q-1)=90 \end{cases} \ < \ =\ > \ $$
$$ \begin{cases} b_2(q+1)=30 \\ q-1=3 \end{cases} \ < \ =\ > \ \begin{cases} q=4 \\ b_2=6 \end{cases} =\ > \ b_1=\dfrac{b_2}{q}=\dfrac{6}{4}=1,5 $$
Ответ: 1,5.Сумма первого и третьего членов геометрической прогрессии равна 10 а сумма второго и четвёртого её членов равна - 20. Найти сумму шести первых членов прогрессии
Как решить?
Решение: $$ \left \{ {{S_1+S_3=10} \atop {S_2+S_4=20}} \right. => \\ \left \{ {{ \frac{2a_1}{2} + \frac{2a_1+2d}{2}\cdot 3 =3 } \atop { \frac{2a_1+d}{2}\cdot 2 + \frac{2a_1+3d}{2}\cdot 4=20 }} \right. =\ > \ \left \{ {{4a_1+3d=10} \atop {6a_1+7d=20}} \right. =\ > \ \left \{ {{a_1= \frac{10-3d}{4} } \atop {6\cdot\frac{10-3d}{4} +7d=20}} \right. $$
$$ 1.5(10-3d)+7d=20\\ 15-4.5d+7d=20\\ 2.5d=5\\ d=2\\ a_1= \frac{10-6}{4}=1 $$
Сумма 6 членов
$$ S_6= \frac{2a_1+5d}{2}\cdot 6=6a_1+15d=6\cdot 1+15\cdot 2 =36 $$
Ответ: 36.