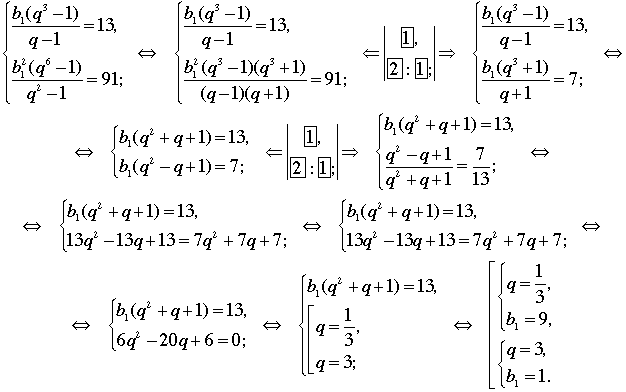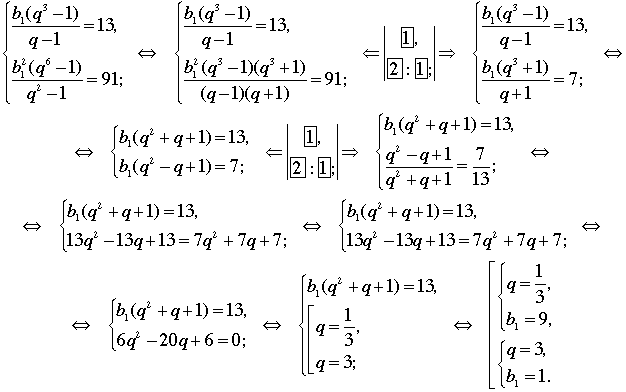прогрессия »
второй член геометрической прогрессии - страница 13
В геометрической прогрессии сумма первого и второго членов равна 84 а сумма второго и третьего членов равна 112. Найти первые три члена этой прогрессии.
Решение: B1+b2=84 b1+b1q=84 b1(1+q)=84 1+q=84/b1 1+q=84/b1 1+q=84/b1
b2+b3=112 b1q+b1q^2=112 b1q(1+q)=112 b1q* 84/b1=112 q*84=112 q=112/84
1+4/3=84/b1 7/3=84/b1 b1=84:7/3 b1=84*3/7 b1=36
q= 4/3 q=4/3 q=4/3 q=4/3 q=4/3
b2=b1*q=36*4/3=48
b3=b1*q^2=36*(4/3)^2=36*16/9=64
Ответ: b1=36;b2=48;b3=64В геометрической прогрессии сумма первого и второго членов равна 140, а сумма второго и третьего членов равна 105. Найдите первые три члена этой прогрессии.
Решение: $$ b_1+b_1\cdot q=140 \\ b_1(1+q)=140 \\ b_1\cdot q \\ b_1\cdot q+b_1\cdot q^{2}=105 $$$$ b_1\cdot q(1+q)=105 $$
$$ b_1=\frac{140} {1+q} $$
$$ \frac {140}{1+q}\cdot q(1+q)=105 $$
14$$ 140\cdot q=105 $$
q=0.75
$$ b_1=\frac{140}{1+0.75}=80 \\ b_2=80\cdot 0.75=60 \\ b_3=60\cdot 0.75=45 $$
В геометрической прогрессии сумма первого и второго членов равна 48, а сумма второго и третьего членов равна 144. Найдите первые три члена этой прогрессии.
Решение: B1 + b2 = 48 b1 + b1q = 48 b1(1 + q)= 48 (*)
b2 + b3 = 144 b1q + b1q² = 144 b1(q + q²) = 144 Разделим 2-е уравнение на 1-е, b1 сократится
(q + q²)/(1 +q) = 3
q(1 + q)/(1 +q) = 3
q = 3
Подставим q = 3 в любое уравнение( например, в (*)
Получим: b1(1 +3) = 48
b1·4 = 48
b1 = 12
Ответ: 12; 36; 108$$ \left \{ {{b_{1}+b_{2}=48} \atop {b_{2}+b_{3}=144}} \right. $$
$$ \left \{ {{b_{1}+b_{1}*q=48} \atop {b_{1}*q+b_{1}*q^{2}=144}} \right. $$
$$ \left \{ {{b_{1}*(1+q)=48} \atop {b_{1}*q*(1+q)=144}} \right. $$
$$ \left \{ {{b_{1}*(1+q)=48} \atop {48q=144}} \right. $$
$$ \left \{ {{b_{1}= \frac{48}{1+q}} \atop {q=3}} \right. $$
$$ \left \{ {{b_{1}= \frac{48}{4}=12} \atop {q=3}} \right. $$
$$ b_{2}=b_{1}*q=12*3=36 $$
$$ b_{3}=b_{2}*q=36*3=108 $$
Ответ: 12; 36; 108
В геометрической прогрессии сумма первого и второго членов равна 40, а сумма второго и третьего членов равна 120. Найдите первые три члена этой прогрессии.
Решение: Из условия имеем b1+ b2=40, а b2+ b3=120
Т. к. b2=(b1 умножить на q), а b3=(b1 умножить на q^2), получаем
b1 + b2= b1 умножить на (1+q)=40
b2 + b3= b1 умножить на (q+q^2)=120 вынесем q за скобку, получим
b2 + b3= b1 умножить на q(1+q)=120, т. к. b1 умножить на (1+q)=40, то q =120/40=3 Найдём b1 из выражения b1 умножить на (1+q)=40
(1+3)b1=40, т. е. 4b1 =40 или b1=10
Чтобы найти сумму первых трёх членов прогрессии достаточно к сумме
(b2 + b3) добавить 10. Т. е 120+10=130
Ответ: 130.
Найти первый член геометрической прогрессии, если сумма первых трех членов прогрессии равна 13, а сумма квадратов первого, второго и третьего членов равна 91.
Решение: Имеем геометрическую прогрессию (bn), в которой первый член b1 и знаменатель q. По условию задачи:b1+b1q+b1q2=13 и. Очевидно, что квадраты членов прогрессии (bn) образуют другую геометрическую прогрессию, первый член которой равен, а знаменатель q2. Записав формулы суммы первых трех членов каждой прогрессии, получим систему уравнений: дальше смотри картинку
Таким образом, условию задачи удовлетворяют две геометрические прогрессии. и вот первые члены 9 и 1