прогрессия »

второй член геометрической прогрессии - страница 6

  • 1. Найдите скалярное произведение векторов а и в, если |а|=5,|в|=4 и 60°-угол между векторами а и в.
    2. найдите 4 числа, которые образуют геометрическую прогрессию. Третий член данной прогрессии больше первого на 9, а второй больше четвертого на 18.
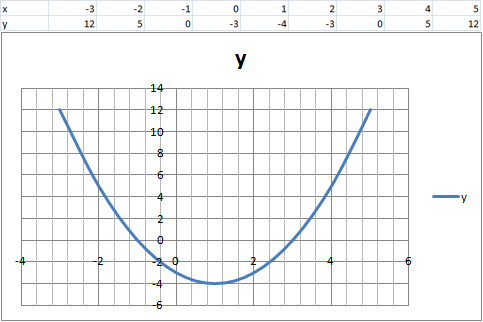
    3. Постройте график функции у=х^2-2х-3. Пользуясь графиком, найдите:
    А) область значения функции;
    Б) промежуток убывания функции.


    Решение: 2) a₁, a₂, a₃, a₄ - 
    a₁, a₁q, a₁q², a₁q³
    a₁q²-a₁=9, a₁(q²-1)=9 (1)
    a₁q³-a₁q=18 a₁q(q²-1=18 (2) поделим (1) на (2) и получаем
    ______________________
    1/q=1/2
    q=2
    a₁(2²-1)=9, a₁=3, a₂=3*2=6, a₃=6*2=12, a₄=12*2=24
    Ответ: 3, 6, 12, 24
    3) график на отдельном листе
    А) область значения: [-4; +∞)
    Б) промежуток убывания функции: (-∞; 1]

    a a a a - a a q a q a q a q -a a q - a q -a q a q q - поделим на и получаем q q a - a a a a Ответ график на отдельном листеА область значения - Б промежуток убывания функции...

  • Второй и пятый члены геометрической прогрессии соответственно равны 24.5 и 196. Найдите члены прогрессии, заключенные между ними.


    Решение: составляем систему уравнений, согласно формуле

    а n-ная =а 1-ая * q в степени n-1 (у тебя в учебнике она есть)

    система уравнений:

    24.5=а1*q в первой степени

    196=а1*q в четвертой степени

    а1=24.5/q

    196=24.5*q четверт степ /q 

    196=24.5*q 3 степ

    q 3 степ=196/24.5

    q 3 степ=8

    q=корень кубический из 8

    q=2

    а3=24.5*2=49

    а4=49*2=98

    ответ: а3=49 ; а4=98

  • Сумма второго и третьего членов геометрической прогрессии равна 30, а разность четвертого и второго равна 90. найдите первый член прогрессии.


    Решение: B3 = b2*q 
    b4 = b2*q^2 
    система уравнений: 
    b2 + b2*q = 30 
    b2*q^2 - b2 = 90 
    b2*(1 + q) = 30 
    b2*(q^2 - 1) = 90 
    3* (1+q) = q^2 - 1 
    q^2 - 3q - 4 = 0 
    q = 4 или q = -1 
    Для первого варианта (q = 4) будет 
    b2 = 6; b5 = b2 * q^3 = 6 * 64 = 384 
    Для второго варианта (q = -1) решений не будет, т. к. b2 = 30:0 (деление на ноль) 
    Ответ: b5 = 384 (т. е. прогрессия: 3/2; 6; 24; 96; 384;.) 

    b3 = b2*q b4 = b2*q^2 система уравнений: b2 + b2*q = 30 b2*q^2 - b2 = 90 b2*(1 + q) = 30 b2*(q^2 - 1) = 90 3* (1+q) = q^2 - 1 q^2 - 3q - 4 = 0 q = 4 или q = -1 Для первого варианта (q = 4) будет b2 = 6; b5 = b2 * q^3 = 6 * 64 = 384 Для второго варианта (q = -1) решений не будет, т. к. b2 = 30:0 (деление на ноль) Ответ: b5 = 384 (т. е. прогрессия: 3/2; 6; 24; 96; 384;.

  • разность между вторым и первым членами геометрической прогрессии равна -6, а разность между третьим и вторым ее членами равна 12. Чему равна сумма первых пяти членов прогрессии заранее спс)


    Решение: $$ \begin{cases} b_2-b_1=-6\\ b_3-b_2=12 \end{cases}\\ b_2=b_1\cdot q\\ b_2=b_1\cdot q^2\\ \begin{cases} b_1\cdot q-b_1=-6\\ b_1\cdot q^2-b_1\cdot q=12 \end{cases}\Rightarrow \begin{cases} b_1\cdot q-b_1=-6\\ q(b_1\cdot q-b_1)=12 \end{cases}\Rightarrow\\ \Rightarrow \begin{cases} b_1\cdot q-b_1=-6\\ -6q=12 \end{cases}\Rightarrow\begin{cases} -2b_1-b_1=-6\\ q=-2 \end{cases} \Rightarrow\begin{cases} -3b_1=-6\\ q=-2 \end{cases}\\ \begin{cases} b_1=2\\ q=-2 \end{cases} $$

    $$ S_5=\frac{b_1(q^5-1)}{q-1}=\frac{2(-32-1)}{-2-1}=\frac{2(-33)}{-3}=\frac{-66}{-3}=22 $$

  • разность между вторым и первым членами геометрической прогрессии равна 18 а разность между четвертым и третьим равна 162 найдите прогрессию


    Решение: {b₂-b₁=18
    {b₄-b₃=162
    {b₁q-b₁=18
    {b₁q³-b₁q²=162
    {b₁(q-1)=18
    {b₁q²(q-1)=162
    {b₁=18/(q-1)
    {(18/(q-1))*q²(q-1)=162 => 18q²=162
      q²=9
      q₁=3 q₂=-3
    при q₁=3 b₁=18/(q₁-1)=18/(3-1)=18/2=9
    при q₂=-3 b₁=18/(q₂-1)=18/(-3-1)=18/(-4)=-4,5
    (bn) 9;27;81;. и (bn) -4,5;13,5;-40,5;.
     

<< < 456 7 8 > >>