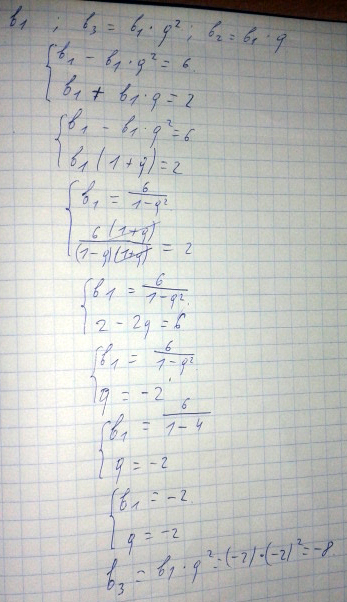второй член геометрической прогрессии - страница 7

разность между первым и третьим членами геометрической прогрессииравна 6. Сумма первого и второго её членов равна 2. Найдите третий член этой прогрессии.

{b1+b2=2

{b1-b1*q^2=6

{b1+b1*q=2

{b1(1-q)=6

{b1(1+q)=2

{b1(1-q^2)=6

{b1(1+q)=2

{b1(1-q)(1+q)=6

{b1(1+q)=2

2(1-q)=6

1-q=3

q=-2

b1(1-2)=2

b1*(-1)=2

b1=-2

b3=b1*q^2=-2*(-2)^2=-8

а1, а2 = a1*q, a3 = a1*q²

a1 - a1*q² = 6

a1 + a1*q = 2

a1 (1-q²) = 6

a1 (1+q) = 2

разделим 1e на 2e

1(1-q)(1+q)/a1(1+q) = 6/2

1-q = 3

q = -2

a1(1+q) = 2

a1 = 2/(-1) = -2

прогрессия: -2, 4,8.

Третий член прогрессии -8

разность между первым и третьим членами геометрической прогрессии равна 6. сумма первого и второго ее членов равна 2. найдите третий член этой прогрессии.

{b1+b2=2

b3-

{b1-b1*q^2=6

{b1+b1q=2

{b1(1-q^2)=6

{b1(1+q)=2

 6/(1-q^2)=2/1+q

6/(1-q)(1+q)=2/(1+q)

6=2(1-q)

1-q=3

q=1-3

q=-2

b1=-2

значит 

b3=b1*q^2=-2*4=-8

Ответ -8

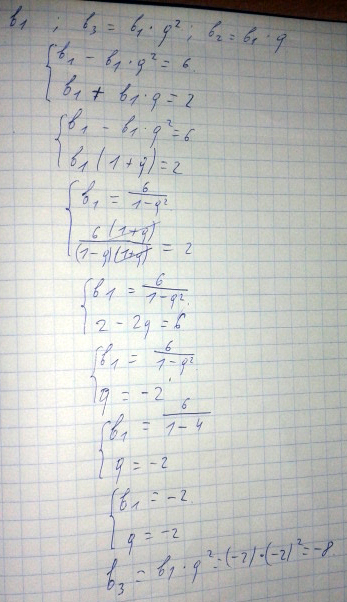
Сумма первого и последнего члена возрастающей геометрической прогрессии равна 66, произведение второго и пятого членов равно 128, сумма всех членов равна 126. найти число членов прогрессии

b1+b1*q^n-1=66 b1*q*b1*q^n-2=128

 b1+b1*q^n-1=66 b1^2*q^n-1=128

q^n-1=x

b1*(1+ x) b1^2*x=128

 решаете систему этих двух уравнений.

получаете ур-ние: 31x^2-1025x+32=0

по дискриминанту получаете:

х1=1/32 х2 = 32

т. к. прогр возраст, то х2 - удовлетвор усл

из второй формулы получаете: b1=корень из 128/х

b1 = 2

Sn=b1*(q (в степени N) - 1) /q-1

получается:

126=2*(32q-1)/(q-1) 

q=2

 q в степени n-1= x

n=6 

В геометрической прогрессии сумма первого и пятого членов равна 51, а сумма второго и шестого равна 102. Несколько членов данной прогрессии сложили и получили число, равное 3069. Количество членов этой прогрессии, которые сложили, нужно найти.

$$ b_1+b_5=b_1+b_1\cdot q^4=b_1(1+q^4) $$

$$ b_1(1+q^4)=51 $$

$$ b_2=b_1\cdot q $$

$$ b_6=b_1\cdot q^{6-1}=b_1\cdot q^5 $$

$$ b_2+b_6=b_1\cdot q+b_1\cdot q^5=b_1\cdot q(1+q^4) $$

$$ b_1\cdot q(1+q^4)=102 $$

$$ 51q=102 $$

$$ q=102:51 $$

$$ q=2 $$

$$ b_1(1+q^4)=b_1(1+2^4)=51 $$

$$ 17b_1=51 $$

$$ b_1=51:17 $$

$$ b_1=3 $$

$$ S_n=b_1\cdot \frac{q^n-1}{q-1} $$

$$ 3069=3\cdot \frac{2^n-1}{2-1} $$

$$ 3069:3=2^n-1 $$

$$ 1023=2^n-1 $$

$$ 1023+1=2^n $$

$$ 1024=2^n $$

$$ 2^{10}=2^n $$

$$ n=10 $$

Ответ: 10.

В знакочередующейся геометрической прогрессии первый член равен 3, а сумма третьего и пятого членов равна 60. Найдите второй член прогрессии?

S = b1(q^2 + q^4) = 60

q^2 + q^4 = 20

q^4 + q^2 - 20 = 0.  По теореме Виета находим возможные значения q^2:

q^2 = -5 - не подходит

q^2 = 4  значит q = -2 ( по условию знакопеременности).

Тогда b2 = b1*q = - 6.

Ответ: - 6.

1. Нам нужно найти знаменатель q, который должен быть отрицательным, т. к. прогрессия знакочередующаяся.

Выражаем третий и пятый члены прогрессии через ее первый член и знаменатель: b3 = 3q²; b₅ = 3q⁴.

Зная, что их сумма равна 60, составляем уравнение:

3q²+3q⁴=60

3q⁴+3q²-60=0 /3

q⁴+q²-20=0 - биквадратное уравнение

q²=t

t²+t-20=0

По теореме Виета: t₁ = -5 - не подходит, т. к. q²≠ -5

  t₂ = 4 ⇒ q²=4

Нас интересует только отрицательный корень. q=-2 

2. Находим b₂.

b₂ = b₁ q

b₂ = 3·(-2) = -6

Ответ.6