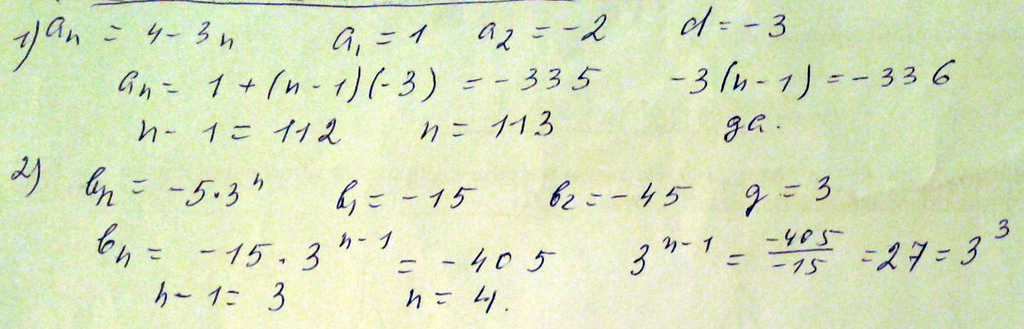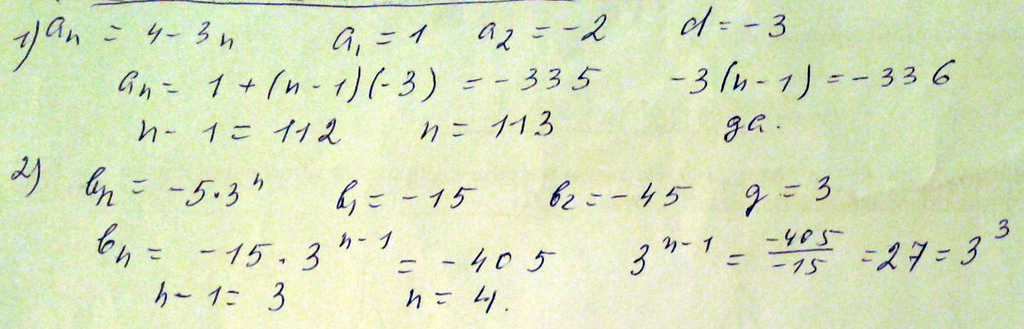n член геометрической прогрессии - страница 11
Три числа, среднее из которых равно 5, составляют арифметическую прогрессию. Если среднее число уменьшить на 20 %, то полученные три числа составляют геометрическую прогрессию. Найдите сумму членов геометрической прогрессии
Решение: Три числа, среднее из которых равно 5, составляют арифметическую прогрессию ==> эти числа 5 - х, 5, 5 + х.
Если среднее число уменьшить на 20 %, получим 4.
и полученные три числа 5 - х, 4, 5 + х составляют геометрическую прогрессию, т. е.
4 = 5 + х
5 - х 4
(5 - х )(5 + х ) = 16
25 - х² = 16
х² = 9
х = 3 или х = - 3
(прогрессии (прогрессии
возрастающие) убывающие)
Cумма членов геометрической прогрессии равна:
S = (5 - 3) + 4 + (5 +3) = 14
Ответ: 14.
Является ли число -1215 членом геометрической прогрессии b_n = -5 *3_n?
Решение: -5*3n=-12153n=243
n=81
ответ -1215, является членом прогрессии
Дано Решение: bn=b1*qn-1
b1=-5 b2=-5*3=-15
q=3 b3=-5*3^2=-45
Найти:(-1215) b4=-5*3^3=-135
b5=-5*3^4=-405
b6=-5*3^5=-1215
Ответ: да является
Является ли число B членом геометрической прогрессии (bn)? Если да, то его номер:
bn=7/9*3n-8, B=63
Решение: Дано: \( b_{n} = \frac{7}{9} *3n-8 \\ b_{n} =63 \)
Найти: \(b_{n}\) ∈ или ∉
если ∈, то \(n=?\)
Решение:
$$ 63= \frac{7}{9} *3n-8 \\ 63+8= \frac{7*3n}{9} \\ 71= \frac{7n}{3} \\ n=71: \frac{7}{3} \\ n=71* \frac{3}{7} = \frac{213}{7} =30 \frac{3}{7} ∉ N \\⇒ b_{n} =63 $$ не является членом прогрессии
Является ли число 424 членом арифметической прогрессии аn=4n+4?
Является ли число 63 членом геометрической прогрессии bn=7/9*3n (/-дробь)
Решение: 1) 424 = 4n+4
420=4n
n=105
n получилось натуральное, значит является членом арифметической прогрессии.
2) Немного непонятно: 3n в знаменателе или вне дроби?
Если в знаменателе: 63=7/(9*3n)
9*3n=7/63
9*3n=1/9
3n=1/81
n=1/243
n - ненатуральное число, членом не является.
Если вне дроби: 63= 7/9 *3n
3n= 63* 9/7
3n=9*9
3n=81
n=27
n - натуральное, членом являетсяаn=4n+4 = 424
4n = 420
n = 105
Ответ: Да, является. 105 член данной прогрессии
bn=(7/9)*3n = 63
n/9 = 3
n = 27
Ответ: Да, является. 27 член данной прогрессии. (если конечно я правильно расшифровал условие и 3n действительно стоит в числителе, а не в знаменателе)
Является ли число а)-335 членом арифметической прогрессии an=4-3n
б) -405 членом геометрической прогрессии bn=-5*3^n
Если является найдите его порядковый номер
Решение: .
1. $$ a_{n}=4-3n; -335=4-3n;\\ 3n=4+335;\\ 3n=339;\\ n=113; $$
да являеться, так как n получилось целое,335 это член даной арифм. прогрессии a(113)=4-3*(113)=4-339=-335
2.$$ b_{n}=-5\cdot3^n;\\ b_{n}=-405;\\ -405=-5\cdot3^n;\\ 3^n= \frac{-405}{-5}=81=3^4;\\ \log_{3}{3^n}=\log_{3}{3^4};\\ n=4; $$
-405 являеться членом геом. прогрессии, при n=4 b4=-5*3^4=-5*81=-405