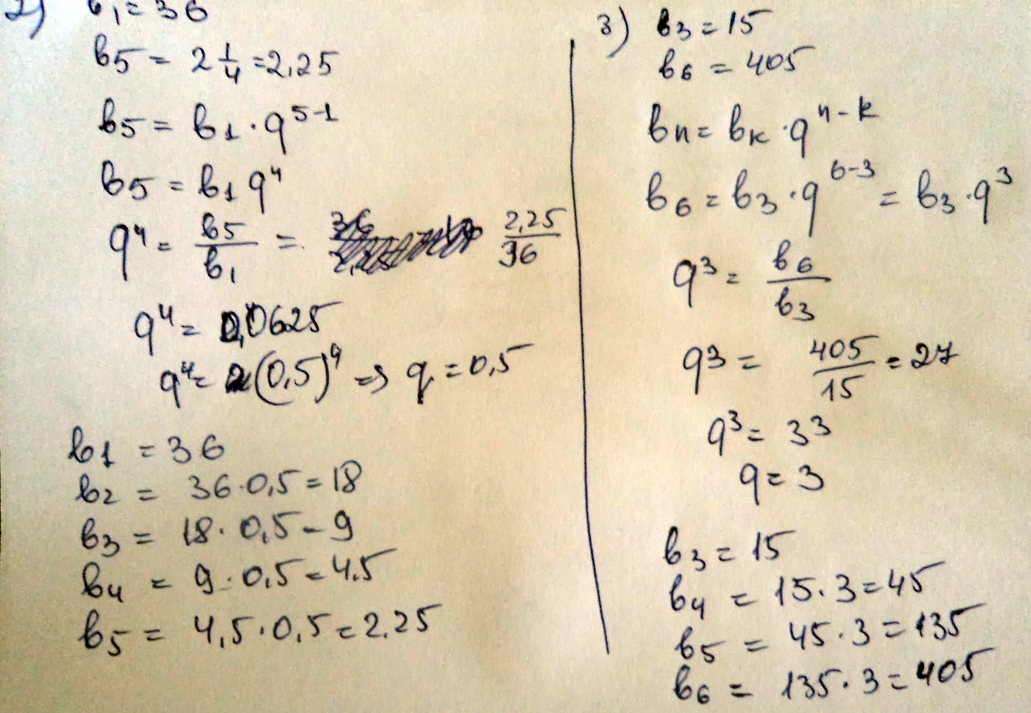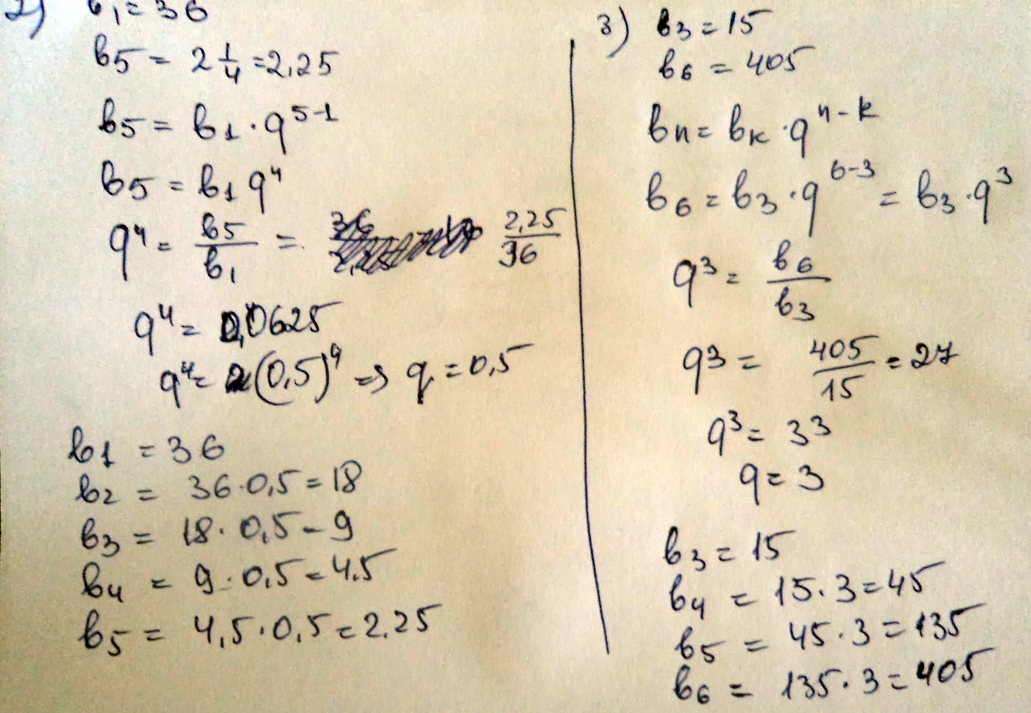n член геометрической прогрессии - страница 12
Какое число не является членом геометрической прогрессиии 1/8; 1/4 А. 40 Б. 4 В. 8 Г. 32.
Решение: А1=1/8
А2=1/4
q=a2/a1=2
A3=a2*2=1/2
A4=a3*2=1
A5=2
A6=4
A7=8
А8=16
А9=32
А10=64
То есть ответ А. 40 не является членом этой прогрессииЧисло 40 не является членом геометрической прогрессии поскольку:
1/8 меньше 1/4 в 2 раза,1/4 меньше 1/2 в 2 раза,1/2 меньше 1 в 2 раза,1 меньше 2 в 2 раза,2 меньше 4 в 2 раза,4 меньше 8 в 2 раза,8 меньше 16 в 2 раза,16 меньше 32 в 2 раза, а 32 меньше 64 в 2 раза, а не 40
1. Найдите b1 и q для геометрической прогрессии (bn) у которой b4=1; b5=-2
2. Найдите девятый член геометрической прогрессии (bn) если b1=1/2; q=-2
3. Является ли число А=243 членом геометрической прогрессии 1/3,1, Если да то укажите его номер.
Решение: 1. b4 = 1
b5 = -2
Найдём знаменатель геометрической прогрессии(q):
q = b5 / b4 = -2 / 1 = -2
По формуле n-ого члена найдём первый член геометрической прогрессии(b1):
b5 = b1 * q^(n-1)
-2 = b1 * (-2)^4
-2 = b1 * 16
b1 = - 0.125
Ответ: q = -2 ; b1 = -0.125
2. b1 = 1/2
q = -2
По формуле n-ого члена найдём девятый член геометрической прогркессии(b9):
b9 = b1 * q^(n-1)
b9 = 1/2 * (-2)^8
b9 = 1/2 * 256
b9 = 128
Ответ: b9 = 128Является ли число A = 1/16 (это дробь) членом геометрической прогрессии 2; 1;. Если да, то укажите его номер.
Решение: Да, является. Она будет 6т. к \(q=\frac{1}{2}\)
a1=2
a2=1
прогрессия геометрическая, найдем знаменатель q:
q=a2/a1=1/2
тогда an=a1*q^(n-1)
Предположим, что 1/16 принадлежит, тогда найдем ее номер:
1/16 = 2*(1/2)^(n-1)
1/32 = (1/2)^(n-1)
(1/2)⁵ = (1/2)^(n-1)
n-1=5
n=6
Таким образом 6 член прогрессии равен 1/16
в геометрической прогрессии одиннадцатый член равен 18, а двенадцатый член равен 6. Найдите десятый член этой прогрессии
Решение: B10=B1*q в степени( n-1)B11=18
B12=6
q=Bn+1/Bn
q=6/18=0.3
B1=q в степени (11)/B12
B1=0.3 в степени (11)/6
а потом подставляете в первую формулу B10=B1*q в степени( n-1)
степени( n-1) это в степени 9
B10=B1*q в степени( n-1)
B11=18
B12=6
q=Bn+1/Bn
q=6/18=0.3
B1=q в степени (11)/B12
B1=0.3 в степени (11)/6
а потом подставляете в первую формулу B10=B1*q в степени( n-1)
степени( n-1) это в степени 9
1) Начиная с какого номера члены геометрической прогрессии 32, 16, 8, меньше 0,01
2) Между числами 36 и 2 1/4 вставьте три пропущенные числа так, чтобы
вместе с данными числами они составили геометрическую прогрессию
3) В геометрической прогрессии третий член равен 15, а шестой - 405. Найдите члены прогрессии, заключенные между ними
Решение: Формула n-ного члена геометрической прогрессии: $$ b_{n} = b_{1} q^{n-1} $$ при n∈N
№1
Используя формулу находим q:
$$ b_{2} = b_{1} q 16=32q q=1/2 $$
Было дано, что члены геометрической прогрессии меньше 0,01, значит составим нер-во:
$$ b_{n} <0,01 $$
$$ 32 * (1/2)^{n-1}<0,01 \\ (1/2)^{-5}*(1/2)^{n-1}<0,01 \\ (1/2)^{n-6}<0,01 $$
Находим подбором степень такую, чтобы само число было меньше 0,01. Это 7
$$ n-6 \geq 7 \\ n \geq 13 $$
№2
$$ b_{1} =36 b_{5} =2,25 \\ b_{5} = b_{1} q^{4} 2,25=36 q^{4} q^{4} =0,0625 \\ q_{1} =0,5 \\ b_{2} =36*0,5=18 b_{3} =36*0,25=\\=9 b_{4} =36*0,125=4,5 q_{2} =-0,5 b_{2} =-18 b_{3} =\\=9 b_{4} =-4,5 $$
№3
$$ b_{3} =15 b_{6} =405 b_{n} =\\= b_{k} * q^{n-k} b_{6} = b_{3} * q^{6-3} q^{3} = \frac{405}{15} =\\=27 q=3 b_{4} =15*3=45 b_{5} =45*3=135 $$