n член геометрической прогрессии - страница 14
Неизвестный положительный член (х) геометрической прогрессии: 0,11; х; 1,76… равен:
Решение: Решение:
Из условия задачи мы знаем:
b1=0,11
b2=x
b3=1,76
Найти: х?
из b2 : b1=q
b3 : b2=q Следовательно:
b2 : b1=b3 : b2
Подставим известные нам значения:
х : 0,11=1,76 : х или:
х*х=1,76*0,11
х²=0,1936
х=+-√1936=+-0,44
х1=0,44
х2=-0,44 -не соответствует условию задачи, так как в этом случае либо первый или третий член геометрической прогрессии был бы задан отрицательным числом
Ответ: х=0,44
Сумма четвертого и пятого членов геометрической прогрессии равна 20, а сумма третьего и четвертого членов равна 5. Найти шестой член прогрессии
Решение: Давайте порассуждаем.
b4 + b3 = 5
b4 + b5 = 20
След. b5 - b3 = 15
b5 = b3q²
b3(q² - 1) = 15
b3(q + 1)(q - 1) = 15
(Ну а b3 - число целое, иначе не получаем указанные суммы. q - рациональное, но (q + 1) и (q - 1) должны быть делителями 15 => q - целое)
15 = 5×3×1
b3(q + 1)(q - 1) = 5×3×1
Тут рассмотрим два случая:
1) b3 = 5
q = 2
b3 + b4 = 5 + 10 = 15 ≠ 5, не подходит
2) b3 = 1
q = 4
b3 + b4 = 1 + 4
b4 + b5 = 4 + 16 = 20
Это нам подходит. Тогда b6 = b5q = 16×4 = 64
Ответ: 64
(хорошая задачка, мне понравилась)Мне, кажется, моё решение чуть проще.
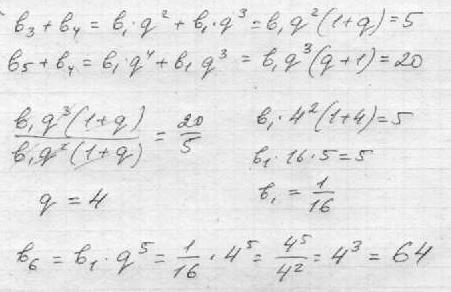
Сумма трех чисел составляющих возрастающую геометрическую прогрессию равна 56. если из них вычесть соответственно 1,7 и 21, то вновь полученные числа составят арифметическую прогрессию. найдите сумму десяти членов геометрической прогрессии. решение нужно?
Решение: Пусть три числа, образующий геометрическую прогрессию, равны соответственно b, bq, bq^2, причем q > 1, т. к. последовательность возрастающая. Тогда b + bq + bq^2 = b(1+q+q^2)=56. Вычтем 1, 7, 21 из членов прогрессии. Получим b-1, bq-7, bq^2-21. Т. к. получилась арифметическая прогрессия, то выполняется условие: (b-1)+(bq^2-21)=2(bq-7)
b(q^2-2q+1)=8.
Разделим одно равенство на другое:
(b(q^2+q+1))/(b(q^2-2q+1))=56/8=7
q^2+q+1=7q^2-14q+7
6q^2-15q+6=0
2q^2-5q+2=0
Далее решаем это квадратное уравнение.
D=(-5)^2-4*2*2=9
q=(5+-3)/(2*2)
q1=2, q2=1/2.
q2 не подходит, т. к. оно меньше 1.
Значит, q=2. Найдем b:
b = 8/(q^2-2q+1)=8/(q-1)^2=8/1=8
Члены геометрической прогрессии: 8,16,32
Члены арифметической прогрессии: 7,9,11. Значит, посчитано правильно.
Теперь найдем сумму первых 10 членов геометрической прогрессии:
S=b*(q^10-1)/(q-1)=8*(2^10-1)/(2-1)=8184Три числа, сумма которых равна 7, составляют возрастающую геометрическую прогрессию. Если бы большее из этих чисел было на 1 меньше, то числа бы составили арифметическую прог. Сколько членов геометрической прогрессии надо взять, чтобы их сумма была равно 255?
Решение: $$ 1) \ a_1 + a_2 + a_3 = 7, \ a_1 = a_1, \ a_2 = a_1q, \ a_3 = a_1q^2,\\\\ a_1 + a_1q + a_1q^2 = 7, \\\\a_1(1 + q + q^2) = 7\\\\ 2) \ a_1 + a_2 + a_3 - 1 = 7 - 1, \ a_2 = a_1 + d, \ a_3 = a_1 + 2d\\\\ \frac{3(a_1 + a_3 - 1)}{2} = 6,^{(*)}\\\\ a_1 + a_3 - 1 = 4,\\\\ a_2 + a_1 + a_3 - 1 = 6,\\\\ a_2 + 4 = 6, \ a_2 = 2\\\\ 3) \ a_2 = a_1q = 2, \ a_1 = \frac{2}{q}, \ q e 0 $$$$ \frac{2}{q}(1 + q + q^2) = 7 \ | * q\\\\ 2 + 2q + 2q^2 = 7q\\\\ 2 - 5q + 2q^2 = 0\\\\ q_1 = \frac{5 - \sqrt{25 - 16}}{4} = \frac{1}{2}, \ q_2 = \frac{5 + \sqrt{25 - 16}}{4} = 2\\\\ 4_{a}) \ a_1 = 4, \ q = \frac{1}{2},\\\\ a_1 + a_2 +. + a_n = 255,\\\\ a_1(1 + q +. + q^{n-1}) = 255,\\\\ S_{n} = 1 + q +. + q^{n-1} = \frac{(q^n - 1)}{q - 1},\\\\ \lim\limits_{n \to +\infty} S_{n} = \frac{1}{q - 1}, \ |q| < 1\\\\ \downarrow\\\\ q e \frac{1}{2} $$
$$ 4_{b}) \ a_1 = 1, \ q = 2,\\\\ a_1 + a_2 +. + a_n = a_1(1 + q +. + q^{n-1}),\\\\ 1 + 2 +. + 2^{n-1} = 255,\\\\ \frac{2^{n} - 1}{2 - 1} = 255,\\\\ 2^{n} = 256,\\\\ 2^{n} = 2^{8}\\\\ \boxed{n = 8} $$
(*) - формула для суммы арифметической прогрессии: $$ S_n = n*\frac{a_1 + a_n}{2} $$
Найдите каждый член геометрической прогрессии, если известно, что сумма двух крайних членов равна 13, а сумма двух средних 4.
Решение: В1; в2; в3: в4- геометрическая прогрессия. составим систему
в1+в4=13. в2+в3=4.
в1+в1q^3=13.
b1q+b1q^2=4.
b1(1+q^3)=13
b1(q+q^2)=4. разделим 1- уравнение на 2- е.
(1+q^3):q(1+q)=13/4. разложим числительюна множители:
(1+q)(1-q+q^2)/q(1+q)=13/4
1-q+q^2 /q=13/4
4( 1-q+q^2)=13q
4-4q+4q^2-13q=0
4q^2-17q+4=0
D=17^2-4·4·4=289-64=225=15^2.
q1=17+15/8=4. q2=17-15/8=1/4. нашли два значения q, теперь найдем члены прогрессии при:
1)q1=4. b1(1+q^3)=13
b1=13/(1+q^3). b1= 13/(1+64)=13/65=1/5=0,2
b1=0,2. b2=0,8. b3=3,2
b4=12,8.
2)q2=1/4.
b1=13/(1+1/64)=64/5=12,8
b2=3,2.
b3=0,8. b4=0,2.