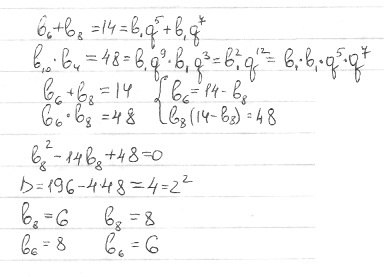n член геометрической прогрессии - страница 15
Найдите 6-й и 8-й член геометрической прогрессии если их сумма равна 14 а произведение 10-го и 4-го членов этой прогрессии равно 48
Решение: эти 6-й и 8-й члены геометрической прогрессии равны 6 и 8, но вот какой из них чему зависит от ттого - убывает эта прогрессия или возрастает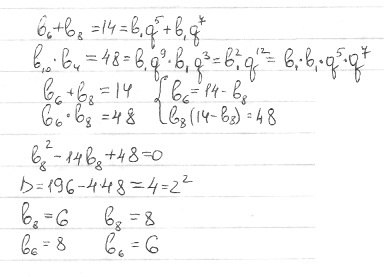
Найдите 7-й и 15-й члены геометрической прогрессии, если их сумма равна 22, а произведение 12-го и 10-го членов этой прогрессии равно 105.
Решение: b7=b1*q^6b15=b1*q^14
b12=b1*q^11
b10=b1*q^9
Любой элемент последовательности равен b(n)=b1*q^(n-1)
(b1*q^6)+(b1^q^14)=22
(b1*q^11)*(b1*q^9)=105
Получили систему с двумя неизвестными
b1*(q^6)(1+q^8)=22
(b1^2)*q^20=105
Поделим второе ур-е на первое два раза
q^8/(1+q^8)^2=105/(22^2)
Находите отсюда q, подставляете и находите b1, а потом искомые числа
1) Найдите наибольший член последовательности a_n=(n^2-14)/2^n
2) Найдите седьмой и четырнадцатый члены возрастающей геометрической прогрессии, если их сумма равна 21, а произведение десятого и одиннадцатого членов этой прогрессии равно 98
Решение: 1). $$ a_{n}\ =\ \frac{n^2-14}{2^n},\ \ \ \ a’(n)=\frac{2n*2^n\ -\ (n^2-14)*2^n*ln2}{2^{2n}}\ = $$$$ =\ \frac{2n-(n^2-14)ln2}{2^n}\ =\ 0,\ \ \ \ln2*n^2-2n-14ln2\ =\ 0, $$
$$ D=4+56ln^22,\ \ \ \ n=\frac{2+\sqrt{4+56ln^22}}{2ln2}\ \approx\ 5,45 $$
Значит нам надо проверить n = 5, и n = 6, и выбрать наибольшее:
Проверка показывает, что $$ a_{5}\ =\ a_{6}= \ \frac{11}{32}.\ $$
Ответ: $$ \frac{11}{32}. $$
2) Пусть х - 7-ой член последовательности, тогда х*q^7 - 14-й член последовательности, а xq^3 и xq^4 - 10-ый и 11-ый члены последовательности. Из условия получим систему:
$$ x(1+q^7)\ =\ 21 $$ $$ x\ +\ \frac{98}{x}\ =\ 21 $$
$$ x^2\ q^7\ =\ 98 $$ $$ q^7\ =\ \frac{98}{x^2} $$
$$ x^2\ -\ 21x\ +\ 98\ =\ 0,\ \ \ \ x_{1}=7,\ \ \ x_{2}=14 $$
Тогда: $$ q_{1}^7\ =\ 2,\ \ \ q_{2}^7\ =\ 0,5 $$
Второе значение не подходит по условию возрастания последовательности.
Итак имеем: $$ x\ =\ b_{7}\ =\ 7,\ \ \ \ \ \ q^7\ =\ 2,\ \ \ \ \ \ b_{14}\ =\ 14. $$
Ответ: 7; 14.
А) Даны четыре последовательных члена геометрической последовательности. Сумма двух крайних членов ровна 13, двух средних равна 4. Определите эти члены
б) Даны три последовательных члена геометрической прогрессии. Их сумма ровна 19, а сумма их квадратов равна 133. Определите эти члены.
Решение: А) Четыре последовательных члена геометрической прогрессии:
b, bq, bq², bq³.
$$ \left \{ {{b+bq^3=13} \atop {bq+bq^2=4}} \right. \\ \left \{ {{b(1+q^3)=13} \atop {bq(1+q)=4}} \right. \\ \left \{ {bq(1+q)=4} \atop {\frac{1-q+q^2}{q}=\frac{13}{4}} \right. \\ \left \{ b=\frac{4}{q(1+q)} \atop {4-4q+4q^2=13q} \right. \\ \left \{ {4q^2-17q+4=0} \atop b=\frac{4}{q(1+q)} \right. $$
4q² - 17q + 4 = 0
D = 289 - 64 = 225
q = 1/4 или 4
Если q = 1/4, тогда $$ b_{1}= \frac{4}{ \frac{1}{4}*(1+\frac{1}{4})}= \frac{64}{5},b_{2}=\frac{16}{5},b_{3}=\frac{4}{5},b_{4}=\frac{1}{5} $$.
Если q = 4, тогда $$ b_{1}= \frac{4}{4*(1+4)}=\frac{1}{5}, b_{2}=\frac{4}{5}, b_{3}=\frac{16}{5}, b_{4}=\frac{64}{5} $$.
Т. е. в обоих случаях члены прогрессии: 1/5, 4/5, 16/5, 64/5.
б) Три последовательных члена геометрической прогрессии: b, bq, bq².
$$ \left \{ {{b+bq+bq^2=19} \atop {b^2+b^2q^2+b^2q^4=133}} \right. \\ \left \{ {{b(1+q+q^2)=19} \atop {b^2(1+q^2+q^4)=133}} \right. $$
$$ \left \{ {{b^2(1+q+q^2)^2=361} \atop {b^2(1+q^2+q^4)=133}} \right. \\ \left \{ {{b^2(1+q^2+q^4+2q+2q^2+2q^3)=361} \atop {b^2(1+q^2+q^4)=133}} \right. $$
$$ \left \{ {{b(1+q+q^2)=19} \atop {2b^2q(1+q+q^2)=228}} \right. \\ \left \{ {{b(1+q+q^2)=19} \atop {bq=6}} \right. $$
$$ \left \{ {{b= \frac{6}{q} } \atop {\frac{6}{q}(1+q+q^2)=19}} \right. \\ \left \{ {{b= \frac{6}{q} } \atop {6+6q+6q^2=19q}} \right. $$
6q² - 13q + 6 = 0
D = 169 - 144 = 25
q = 2/3 или 3/2
Если q = 2/3, тогда $$ b_{1}= \frac{6}{\frac{2}{3}}=9, b_{2}=6, b_{3}=4. $$
Если q = 3/2, тогда $$ b_{1}= \frac{6}{\frac{3}{2}}=4, b_{2}=6, b_{3}=9. $$
Т. е. в обоих случаях члены прогрессии: 4, 6, 9.
Найдите 6-й и 8-й члены геометрической прогрессии если их сумма равна 14, а произведение 10-го и 4-го членов этой прогрессии равно 48
Решение: b6+b8=14b10*b4=48
b6+b8=14
b1*q^9*b1*q3=48
b1^2*q*12=48
(b1*q6)^2=48
(b7)^2=48
Применим характеристическое свойство геометрической прогрессии:
b6*b8=(b7)^2
b6*b8=48
b6=48/b8
b6+b8=14
48/b8 +b8=14
48+(b8)^2=14*b8
(b8)^2-14b8+48=0
b8(1)=6, b8(2)=8 (по теореме Виета)
b6=(1)=48/6=8, b6(2)=48/8=6
Ответ: 6;8 и 8;6