прогрессия »

n член геометрической прогрессии - страница 16

  • Дана геометрическая прогрессия 1;3;9;27. Найдите знаменатель прогрессии и её пятый, шестой и седьмой члены?


    Решение: Воспользуемся определение знаменателя геометрической прогрессии:
    Знаменатель геометрической прогрессии – это число, равное отношению второго и любого последующего члена к предыдущему члену прогрессии. Ее обычно обозначают буквой q. =>
    1. q=$$ \frac{9}{3}=3 $$
    2. Найдем n-й член геометрической прогрессии, использовав базовую формулу:
    Пятый член: 
    $$ b_{5} = 1 * 3^{4} = 81$$
    Седьмой член:
    $$ b_{7} = 1 * 3^{6} = 729$$
    И шестой, уже по известной нам формуле:
    $$ (b_{6}) ^{2} = 729 * 81= 59049 $$
    $$ b_{6} = 243 $$
    Ответ: q=3; 81; 243; 729.

  • дана геометрическая прогрессия 16,8. Найдите сумму её членов с 4 по 7 включительно


    Решение: b1=16

    b2=-8

    Найдём q по формуле:

    $$ q=\frac{b2}{b1}=\frac{-8}{16}=-0,5 $$

    Теперь 4-ый и 7-ой члены:

    $$ bn=b1*q^{n-1} $$

    $$ b4=16*(-0,5)^{4-1}=16*(-0,5)^{3}=16*(-0,125)=-2 $$

    $$ b7=16*(-0,5)^{7-1}=16*(-0,5)^{6}=16*0,015625=0,25 $$

    Теперь пусть b4 - это первый член, тогда b7 - четвёртый, n=4

    Сумма:

    $$ Sn=\frac{b1*(q^{n}-1)}{q-1}=\frac{-2*(0,5^{4}-1)}{0,5-1}=\frac{2*(0,0625-1)}{-0,5}=\frac{-1,875}{-0,5}=3,75 $$

    b1=16
    b2=-8
    q=-8/16=-0,5
    b3=-8*(-0,5)=4
    b4=4*(-0,5)=-2

    b5=-2*(-0,5)=1

    b6=1*(-0,5)=-0.5

    b7=-0.5*(-0,5)=0.25
    b4+b5+b6+b7=-2+1+(-0.5)+0.25=-1.25

  • Даны три члена геометрической прогрессии:2,x,18 найдите x если x<0


    Решение: Очень просто х = 6
    Как решать. Каждый член прогрессии равен предыдущему умноженному на какое либо число. К примеру, а пусть будет. А первый пусть будет 2 как у тебя в задаче. Тогда 2-ой член будет равен 2*а, а 3-ий 2*а*а из 3 мы легко находим а. а^2=3-ий/1-ий тогда а^2=9 Откуда а =3. А 2-ой член равен 2*а как мы и говорили и это получается 2*3=6

  • Дана геометрическая прогрессия : 16,8,
    Найдите сумму ее членов с четвертого по седьмой включительно


    Решение: q=b2/b1=-1/2

    ^ - значек степени

    S7=16(-1/2^7-1)/(-1/2-1)=43/4

    S3=16(-1/2^3-1)/(-1/2-1)=12

    S(4.7)=S7-S3=43/4-12=43/4-48/4=-5/4

    Знаменатель прогресси q=-8/16=-2

    четвертый член b4=b1*q^(4-1)=16/-8=-2

    Сумма с четвертого по седьмой это 4, 5, 6, 7 - 4 штуки, начиная с четвертого.

    S=b4(q^4-1)/(q-1)

    S=-2((-1/2)^4-1)/((-1/2)-1)

    S=-2((-1/2)^4-1)/((-1/2)-1)

    S=-30*2/(16*3)=-60/48=-1целая и 1/

  • 1. \( \frac{4}{ \sqrt{2}+1 } - \sqrt{32} \)
    2. дана геометрическая прогрессия : 16,8, найдите сумму ее членов с четвертого по седьмой включительно
    3.\( \left \{ {{7-x< 1-4x} \atop {18+2x \geq -3-5x}} \right. \)


    Решение: 1. $$ \frac{4}{\sqrt{2}+1}-\sqrt{32}=\frac{4(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}-4\sqrt{2}=\frac{4\sqrt{2}-4}{2-1}-4\sqrt{2}= \\ =4\sqrt{2}-4-4\sqrt{2}=-4 $$
    2. Тупо выпишем члены с первого по седьмой. $$ b_n=\{16;-8;4;-2;1;-\frac{1}{2};\frac{1}{4};.\} $$
    Наша сумма равна $$ -2+1-\frac{1}{2}+\frac{1}{4}=-1-\frac{1}{4}=-\frac{5}{4} $$
    3.$$ \left \{ {{7-x<1-4x} \atop {18+2x\geq -3-5x}} \right. $$.
    Работаем с каждым неравенством как с уравнением, т. е. будем переносить слагаемые и делить на числа, причем если делим на отрицательное, то мы меняем знак на противоположный.
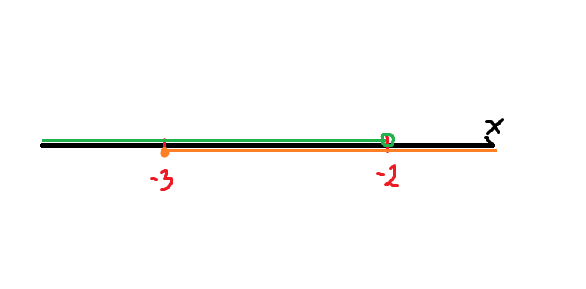
    $$ \left \{ {{3x<-6} \atop {7x\geq -21}} \right. \\ \left \{ {{x<-2} \atop {x\geq-3}} \right. $$
    Зеленым - первое неравенство, оранжевым - второе. Где же они пересекаются? Правильно - на отрезке $$ [-3;-2) $$! Там, где точка не учитывается (выбитая точка, или дырка от бублика), там ставим круглую скобку, На включаемую точку ставим квадратную - ведь точка -3 удовлетворяем обоим неравенствам. Собственно, $$ x \in [-3;-2) $$ и будет решением.

    .  frac sqrt - sqrt frac sqrt - sqrt sqrt - - sqrt frac sqrt - - - sqrt sqrt - - sqrt - . Тупо выпишем члены с первого по седьмой.  b n - - - frac frac . Наша сумма равна  -...
<< < 141516 17 18 > >>