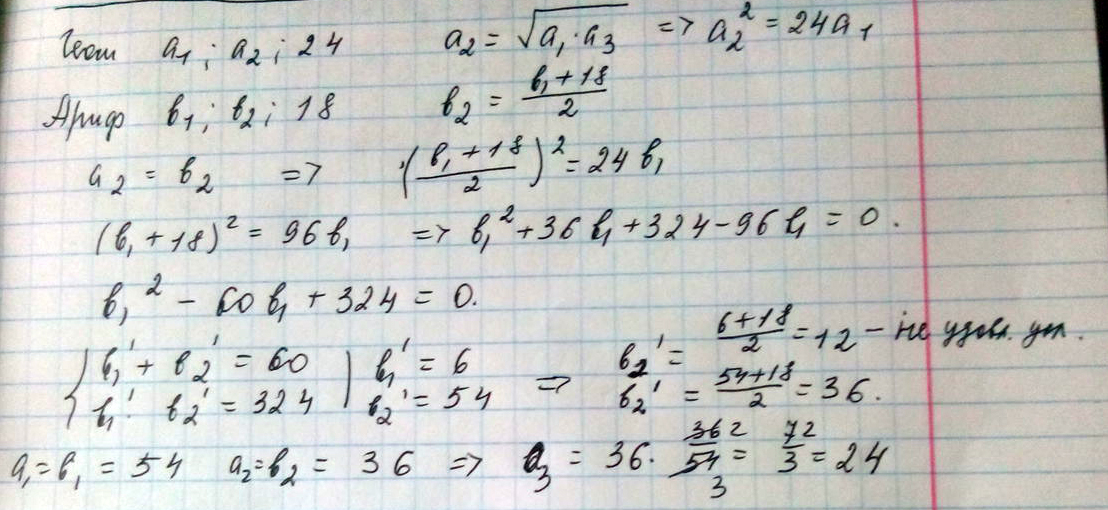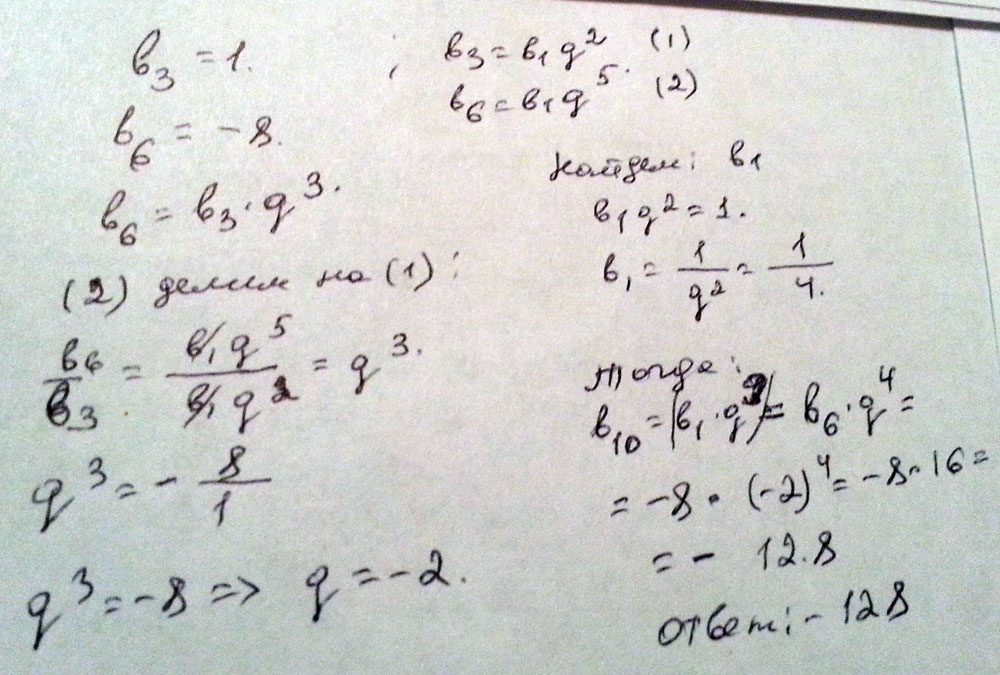прогрессия »

n член геометрической прогрессии - страница 13

  • найдите шеснадцатый член геометрической прогрессии, третий член которой равен 3, а пятый равен 27


    Решение: возможно такое решение:

    есть формула: Bn=B1*q^(n-1)

    Если известен третий и пятый член, то можно вычислить q, q=3

    И можем найти первый член(B1), который нам необходим. Он равен 1/3

    Подставляем в формулу:

    B16= 1/3* 3^(16-1)

    B16=3^14

    Ответ: шестнадцатый член 3^14

    (b[n]=b[1]q^(n-1))

    b[3]=3

    b[5]=27

    b[5]=b[4]q=b[3]q^2

    q^2=b[5]/b[3]

    q^2=27/3

    q^2=9

    q=3 или q=-3

    1 случай

    если q=3, то

    b[1]=b[3]/q^2

    b[1]=3/3^2=1/3

    b[16]=b[1]q^(16-1)=b[1]q^15

    b[16]=1/3*3^15=3^14 (если требуется точное число то это 4 782 969, хотя по идеи результат можно сохранить в виде 3^14)

    2 cлучай

    если q=-3, то

    b[1]=b[3]/q^2

    b[1]=3/(-3)^2=1/3

    b[16]=b[1]q^(16-1)=b[1]q^15

    b[16]=1/3*(-3)^15=-3^14

    ответ: -3^14 или 3^14

  • В убывающей геометрической прогрессии, состоящей из 3 членов, третий член равен 24. Если вместо третьего числа поставить 18, то образуется арифметическая прогрессия.


    Решение: $$ Geometr.\; progressiya:\; \; b_1,\; b_2,\; b_3=24,\\\\b_2^2=b_1\cdot b_3\; \; \to \; \; b_2^2=24b_1\\\\Arifm.\; progr.\; :a_1,\; a_2,\; a_3,;\; \; \; a_1=b_1,\; a_2=b_2,\; a_3=18\\\\a_2=\frac{a_1+a_3}{2}\; \;\to \; \; b_2=\frac{18+b_1}{2}\\\\b_2^2=\frac{(18+b_1)^2}{4}=24b_1\\\\324+36b_1+b_1^2=96b_1\\\\b_1^2-60b_1+324=0\\\\D/4=576,\; \sqrt{D/4}=24\\\\b_1=54\; \; ili\; \; b_1=6 $$
    $$ 1)\; \; b_1=54,\; b_2=\frac{18+b_1}{2}=\frac{18+54}{2}=36,\; b_3=24\; \; -\; otvet\\\\2)\; \; b_1=6,b_2=\frac{18+6}{2}=12,\; b_3=18\; \; \to \; \; ne\; geom.\; progr. $$


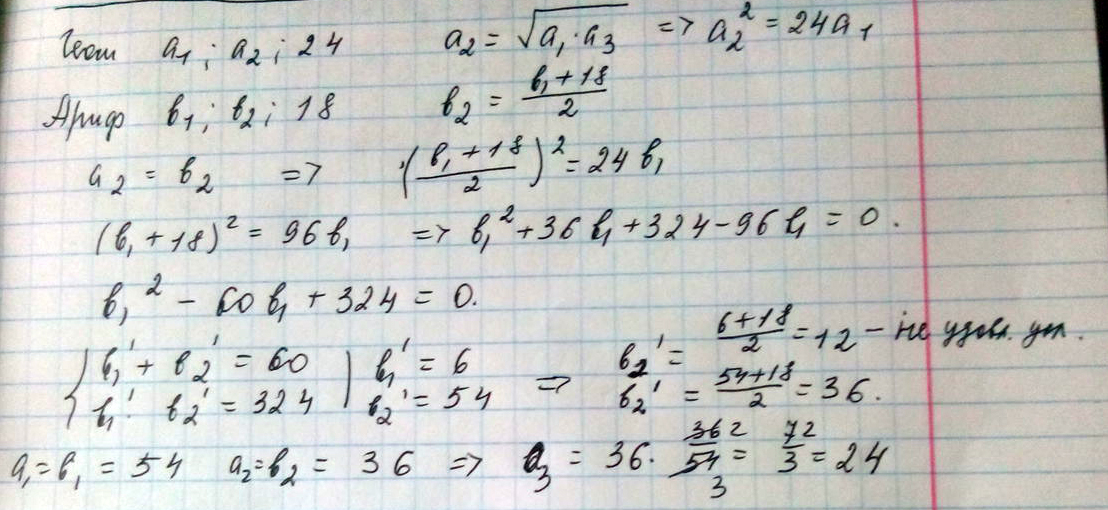
    Geometr. progressiya b b b b b cdot b to b b Arifm. progr. a a a a b a b a a frac a a to b frac b b frac b b b b b b - b D sqrt D b ili b b b frac b frac b - otvet b b frac b...

  • Найдите 10 член геометрической прогрессии если третий член равен 1, а шестой равен - 8


    Решение: Логикой можно догадаться что q=-2
    1*(-2)=-2
    -2*(-2)=4
    4*(-2)=-8 шестой
    -8*(-2)=16
    16*(-2)=-32
    -32*(-2)=64
    64*(-2)=-128 десятый

    Ответ в приложении

    Логикой можно догадаться что q - - - - - - - шестой- - - - - - - - десятый Ответ в приложении...

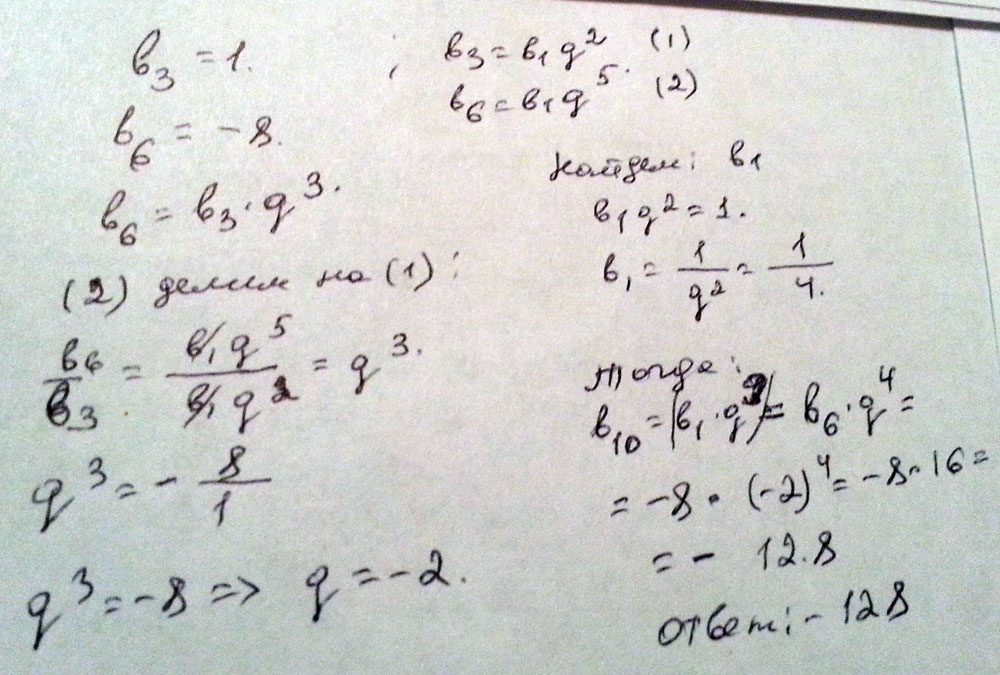
  • Найдите десятый член геометрической прогрессии, если третий член равен 1, а шестой -8


    Решение: а₆=4

    а₄=9

    разложим по формуле

    а₁+5д=4

    а₁+3д=9

    получилась система

    отсюда 

    найдем д

    -2д=5

    д=5+2

    д=7

    найдем а₁, подставим д=7 в 1 уравнение

    а₁+35=4

    а₁=-31

    найдем а₇

    а₇=(-31)+6*7=-31+42=11

    а₇=11

  • Найдите десятичный член геометрической прогрессии если ее третий член равен 1 а шестой равен минус 8


    Решение: а1=?

    а3=5

    а8=-10

    а3=а1+2d

    a8=a1+7d

    5=a1+2d

    -10=a1+7d

    отнимаем систему

    15=-5d

    d=-3

    теперь подставляем d и находим а1

    5=a1-6

    a1=11

    -10=a1-21

    a1=11

    Bn) - геометрическая прогрессия.
    Дано:
    b4 = 24,
    b6 = 54.
    Найти: b5.
    Решение:
    bn = b1 * q^(n-1)
    b6 = b4 * q^2
    q^2 = b6/b4 = 54/24 = 9/4 = 2,25
    q = √2,25 = 1,5
    b5 = b4 * 1,5 = 24 *1,5 = 36.
    Ответ: b5 = 36.
    ^ – это степень.

<< < 111213 14 15 > >>