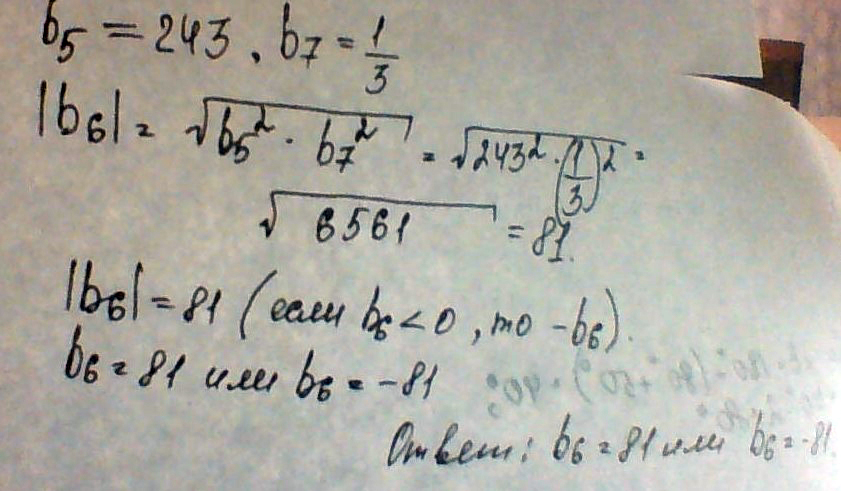n член геометрической прогрессии - страница 22
Дано: 625; 125; ...; 1/25
Нужно найти n последнего члена геометрической прогрессии.
Решение: B1=625
b2=125
q=b2/b1=1/5
bn=1/2
bn=b1*q^(n-1)
1/25=625*1/5^(n-1)
1/25*1/625=1/5^(n-1)
1/(25*625)=1/5^(n-1)
5^(n-1)=(25*625)=5^(2+4)=5^6
(n-1)=6
n=7
Решение:
Найдем, чему будет равно частное прогрессии:
$$ q=\frac{b_{n+1}}{b_n} \\ q = \frac{125}{625} = 0.2 $$
Мы нашли частное прогрессии. Пусть x - номер последнего члена.
Тогда решим уравнение относительно формулы:
$$ b_n=b_1q^{n-1} $$
Подставляем известные данные:
$$ 5^{-2}=5^4*0.2^{x-1} \\ 5^{-2}=5^4*5^{1-x} \\ $$
Решаем показательное уравнение. Убираем основания степеней:
$$ -2 = 4 + (1 -x) \\ -2 = 4+1-x \\ 5-x = -2 \\ x = 7 $$
Значит, искомый номер последнего члена равен семи.
Ответ: n = 7
Выписано несколько последовательных членов геометрической прогрессии: b,0.04, 0,2. Найдите член прогрессии, обозначенный через b.
Решение: Геометрическая прогрессия задана условиями: b1=3, bn+1=3bn. Какое из данных чисел является членом этой прогрессии?6 12 24 27 Существует ли геометрическая прогрессия, в которой b2=-2, b5=54, b7=486? В геометрической прогрессии b1=-81, q =. В каком случае при сравнении членов этой прогрессии знак неравенства поставлен неверно?b1<b<b2 b1<b<b3 b2>b4 b3>b5 Известны два члена геометрической прогрессии: b3=12, b4= 24. Найдите сумму первых десяти членов этой прогрессии Выписано несколько последовательных членов геометрической прогрессии:…. Найдите член прогрессии, обозначенный через b. Геометрическая прогрессия задана условиями: b1=3, bn+1=3bn. Какое из данных чисел является членом этой прогрессии?6 12 24 27 Существует ли геометрическая прогрессия, в которой b2=-2, b5=54, b7=486? В геометрической прогрессии b1=-81, q =. В каком случае при сравнении членов этой прогрессии знак неравенства поставлен неверно?b1<b<b2 b1<b<b3 b2>b4 b3>b5 Известны два члена геометрической прогрессии: b3=12, b4= 24. Найдите сумму первых десяти членов этой прогрессии Выписано несколько последовательных членов геометрической прогрессии:….b; Найдите член прогрессии, обозначенный через b. Геометрическая прогрессия задана условиями: b1=3, bn+1=3bn. Какое из данных чисел является членом этой прогрессии?6 12 24 27Пятый и седьмой член убывающей геометрической прогрессии равны соответственно 243 и 1/3. Найдите шестой член прогрессии
Решение: B₅=243
B₇=¹/₃
B₆-
B₇=B₅*q²
q²=B₇
B₅
q²=¹/₃ : 243
q²=¹/₃ * ¹/₂₄₃
q²=¹/₇₂₉
q=¹/₂₇
B₆=B₅*q=243 * ¹/₂₇=9
Ответ: B₆=9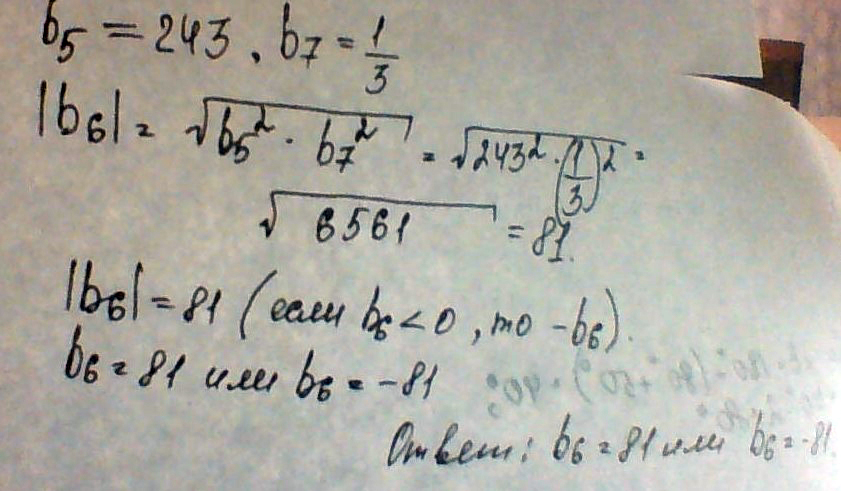
В геометрической прогрессии с четным числом членов сумма всех ее членов в 3 раза больше суммы членов, стоящих на нечетных местах. Найдите знаменатель прогрессии.
Решение: Здесь неясность, в прогрессии количество элементов бесконечно, хотя в убывающей геометрической прогрессии сумма всех элементов может сходиться.Иными словами, условие следует понимать так что n первых членов прогрессии, где n = 2k,
выполняется условие $$ \sum_{k=1}^{\ n/2}(b_{2k}) $$ в три раза больше, чем $$ \sum_{k=0}^{\ n/2}(b_{2k+1}) $$
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
Ответ 3
Найдите три последовательных члена геометрической прогрессии с положительными членами, если их сумма равна 21, а сумма обратных к ним чисел равна 7/12
Решение: Первый из трех обозначим b1
следующий: b1*q
третий: b1*q² (q > 0)
b1 + b1*q + b1*q² = 21
b1*(1+q+q²) = 21 -> b1 = 21 / (1+q+q²)
(1 / b1) + (1 / (b1*q)) + (1 / (b1*q²)) = 7/12
(1 / b1)*(1 + (1/q) + (1/q²)) = 7/12
((1+q+q²) / 21)*((q²+q+1) / q²) = 7/12
(1+q+q²)² = (7/12) * 21q²
((1+q+q²) / q)² = 49/4
(1+q+q²) / q = 7/2 или (1+q+q²) / q = -7/2
2+2q+2q² = 7q или 2+2q+2q² = -7q
2q²-5q+2 = 0 или 2q²+9q+2 = 0
D=25-16=3² D=81-16=65
q1 = (5-3)/4 = 0.5 q3 = (-9-√65)/4 < 0
q2 = (5+3)/4 = 2 q4 = (-9+√65)/4 < 0
1) q = 1/2 - убывающая последовательность
b1 = 21 / (1+0.5+0.25) = 21 / 1.75 = 12
b2 = 12*0.5 = 6
b3 = 6*0.5 = 3 -их сумма = 21
(1/12) + (1/6) + (1/3) = (1/12) + (2/12) + (4/12) = 7/12
2) q = 2 - возрастающая последовательность
b1 = 21 / (1+2+4) = 3
b2 = 3*2 = 6
b3 = 6*2 = 12 -их сумма = 21
(1/12) + (1/6) + (1/3) = (1/12) + (2/12) + (4/12) = 7/12