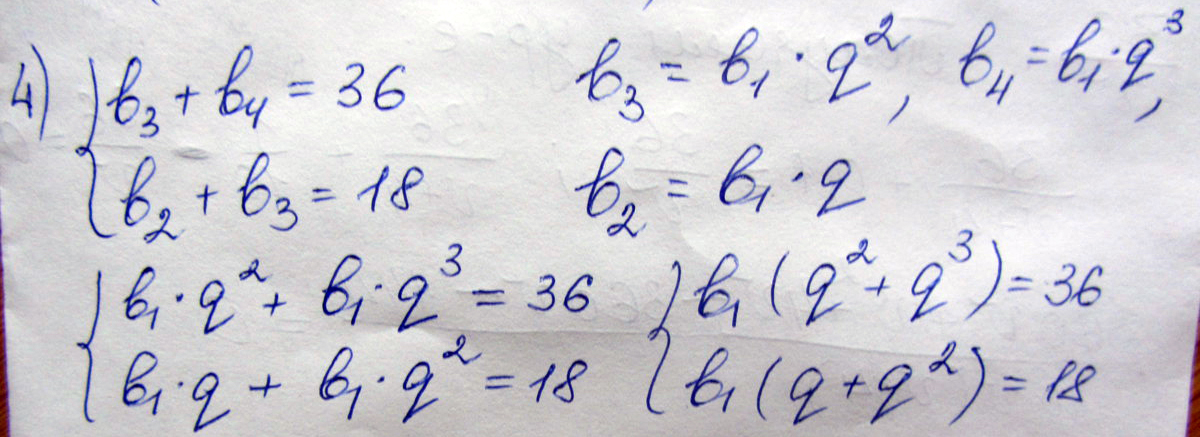прогрессия »

n член геометрической прогрессии - страница 8

  • Три различных числа a,b,c, сумма которых равна 124, являются последовательными членами геометрической прогрессии. Одновременно эти числа a,b,c являются соответственно 3,13 и 15-м членами арифметической прогрессии. Найти a,b,c.


    Решение: Ну легко же, чего такие трудности. 
    Числа можно сразу записать в виде a = x + 3d; b = x + 13d; c = x + 15d;
    раз это геометрическая прогрессия, то b/a = c/b; или b^2 = ac;
    (x + 3d)(x + 15d) = (x + 13d)^2; откуда x = (-31/2)*d;
    Поэтому числа a b c можно записать в виде
    a = d*(-25/2); b = d*(-5/2); c = d*(-1/2); (то есть знаменатель геометрической прогрессии равен 1/5; что в общем-то уже все решает); 
    Если сложить, получится 124. То есть d = -8; и 
    a = 100; b = 20; c = 4; 

  • задание №1 в геометрической прогрессии в1=8, в3=24 найдите в5 ответ :72 задание №2 дана арифметическая прогрессия: 3,3; 2,9. Сколько положительных членов она содержится? ответ: 9


    Решение: 1) b3=b1*q2

    24=8*q2

    q2=3

    q=V3   т. е. кореннь из 3

    b5=b1*(V3)4

    b5=8*9

    b5=72

    2) d=2,9-3,3=-0,4

    an=a1+d*(n-1)

    Отрицательным будет тот член, в котором произведение |d*(n-1)|>a1

    |-0,4n+0,4|>3,3

    |-0,4n|>2,9

    |-4n|>29

    |n|>7,25, то есть проверим а8=3,3-0,4*7=0,5

    а9=3,3-0,4*8=0,1, значит а10 будет отрицательным

    Ответ 9 положительных членов

  • В геометрической прогрессии сумма членов вычиляется по формуле Sn=3(1-2⁻²)

    найти b₁₀


    Решение: $$ Sn=\frac{b_{1}(q^{n}-1)}{q-1} $$

    Приведем данную в условии форулу к стандартному виду:

    $$ Sn=3(1-2^{-2})=3(1-\frac{1}{2^{2}})=3\frac{2^{2}-1}{4} $$

    Отсюда мы можем сказать, что была записана формула суммы 2 членов прогрессии, где 1-й член 3/4, а знаменател прогрессии равен 2

    b10=(3/4)*2^9=(3/4)*512=384

  • Найдите 5 член геометрической прогрессии в которой
    B3+B4=36
    B2+B3=18


    Решение: B₃+b₄=36 ;b₂+b₃=18.
    -
    b₅ ==>?
    {b₁q² +b₁q³ = 36 ; b₁q  +b₁q² =18. {b₁q²(1+q) =36; b₁q(1 +q) = 18.
    {q=2 ;b₁*2(1+2) =18.{b₁=3; q =2.
    b₅ = b₁*q^4 =3*2^4 =48.

    ответ : 48.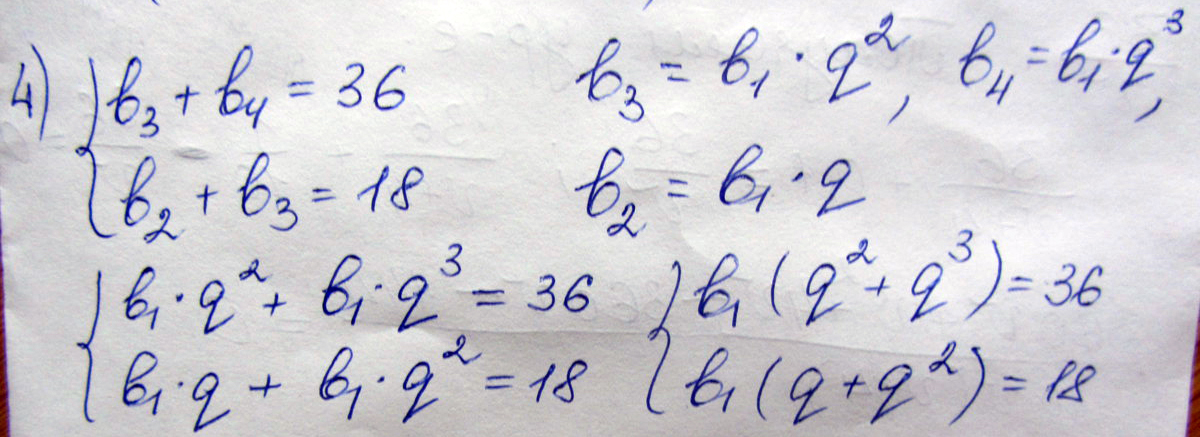

    B b b b .-b gt b q b q b q   b q . b q q  b q q . q b . b q .b  b q .ответ    ....

  • Сумма 1-го и 3-го членов геометрической прогрессии равна 4, сумма 2-го и 4-го её членов равна -12. Найдите 5-й член прогрессии.
    подробнее.


    Решение: По этим 2-м условиям составим систему двух уравнений.
    b1 +b1·q^2 = 4
    b1·q+ b1·q^3 = -12/
    Решаем. b1(1 + q^2) = 4
      b1 q(1 + q^2) = -12 (Делим второе уравнение на первое)
        q = -3
    Теперь этот знаменатель подставим в первое (можно во второе) уравнение
    b1 + 9b1 = 4
    10b1 = 4
    b1 = 0,4
    Теперь можно искать b5
    b5 = b1·q^4 = 0,4·(-3)^4= 0,4·81= 32,4
    b5 = 32,4

<< < 678 9 10 > >>