прогрессия »

найдите n член прогрессии - страница 10

  • Найдите восьмой член арифметической прогресси, если сумма 3-го, 7-го и 14-го равна 15.


    Решение: $$ a_3 = a_1 +2d\\ a_7 = a_1 +6d\\ a_{14} = a_1 +13d\\ a_3+a_7+a_{14} = a_1 +2d +a_1 +6d+ a_1 +13d=3a_1 +21d\\ 3a_1 +21d=15\\ 3(a_1 +7d)=15\\ a_1 +7d=5\\ a_8=a_1 +7d\\ a_8=5\\ $$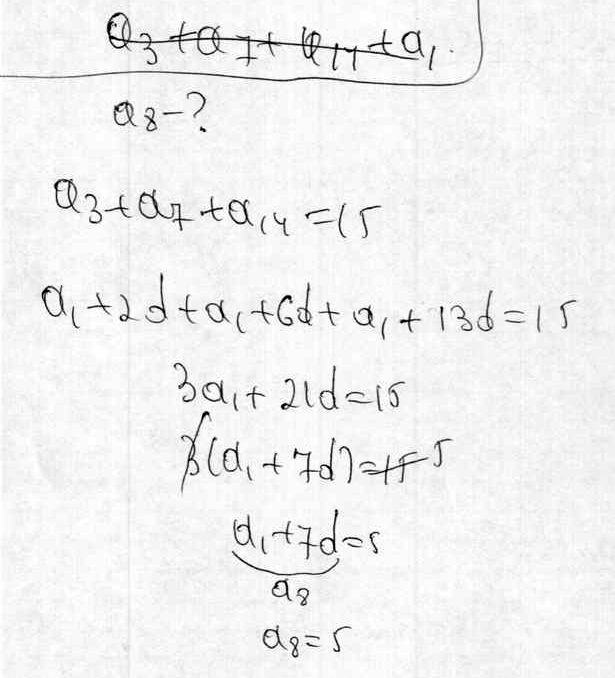

    a a d a a d a a d a a a a d a d a d a d a d a d a d a a d a...

  • 1) Выписано несколько последовательных членов арифметической прогрессии:.;11; х;19;23;. Найдите член прогрессии, обозначенный буквой х. 2) Арифметическая прогрессия (bn) задана формулой bn=17-5n. Какой из следующих чисел не является членом этой прогрессии: 1) 12 2) -3 3)3 4)-13 (с решением)


    Решение: 1. мы используем свойство арефметической прогресси. т. е. сумма предыдущего члена и последующего делим пополам.
    х=(11+19)/2=30/2=15

    2. мы подставляем вместо bn числа.
    а) 12=17-5n
    -5=-5n
    n=1 (т. к. получилось натуральное число, то 12 - является частью прогрессии)
    б) -3=17-5n
    -20=-5n
    n=4 (подходит)
    в) 3=17-5n
    -14=-5n
    n=2,8 (не подходит, не натуральное число)
    г) -13=17-5n
    -30=-6n
    n=5 (подходит)

  • Найдите 5-ый член арифметической прогрессий
    1)19;15;11;.;
    2)-1;2;7;.;
    Найдите 5-ый и n-й члены арифметической прогрессий
    1)1;-1;.;
    3
    2)2,3,1;.;
    3)-8;-6;5;.;
    4)11.7;.;
    Напишите первые четыре члена арифметической прогрессий{аn}
    1) а1=10;d=4;
    2)a1=1,7;d=0,2$
    3)a1=-3,5;d=0,6;
    4)a1=4; d=1 ;
    3 6
    Найдите 1)a11, если а1=-3,d=0,7; 2)a20, если а1=18,d=-0,5; 3)a11, если а1=20,d=9 4)b21, если b1=5,8;d=-1,5;
    a11, а1,b21-это у меня индексы
    Докажите тождество
    1)sin²α·cos²β-cos²α·sinβ=sin²α-sin²β
    2)cos²α·cos²β-sin²α·sin²β=cos²α-sin²β


    Решение: Номер 1.
    1) 19; 15; 11; 7; 3*. (d=-4)
    2) -1; 2; 7 - не является арифм. прогр.
    Номер 2.
    1) 1;-1;-3;-5;-7*. (d=-2)
    n-й член=первый член+d×(n-1)
    2) немного не понятно условие.
    3) Не является арифм. прогр.
    4) нет второго члена для вычисления разности.
    Номер 3.
    1) 10; 14; 18; 22;
    2) 1,7; 1,9; 2,1; 2,3;
    3) -3,5; -2,9; -2,3; -1,7;
    4) 4; 5; 6; 7.
    Номер 4.
    1) а11=-3+0,7×10=4*.
    2) а20=18-9,5=8,5*.
    3) а11=20-90=110*.
    4) b21=5,8-30=-24,2*.

  • 1) Найдите 15 й член прогрессии если d=-3
    2) Найдите a1 и d
    a10=1.9 ;a16=6.1
    3) Найдите S10 2;5;8.
    4) найдите a1=10
    d=4 S8-


    Решение: $$ 2)\;a_{10}=a_1+9d\\a_{16}=a_1+15d\\a_{16}-a{10}=a_1+15d-a_1-9d=6d\\6d=6,1-1,9=4,2\\d=0,7\\a_{10}=a_1+9d\\a_1+9\cdot0,7=1,9\\a_1=1,9-6,3\\ a_1=-4,4\\\\3)\;a_1=2,\;a_2=5,\;a_3=8\\d=a_2-a_1=5-2=3\\S_{10}=\frac{2a_1+9d}{2}\cdot 10=(2a_1+9d)\cdot5=10a_1+45d=10\cdot2+45\cdot3=\\=20+135=155\\\\4)\;S_{8}=\frac{2a_1+7d}2\cdot8=8a_1+28d=8\cdot10+14\cdot4=80+56=136 $$

  • Найдите первый отрицательный член прогрессии: (An): 12,5; 11,2.


    Решение: An=А1+(n-1)d

    An=12.5+(n-1)*(-1.3)

    (Аn)12.5;11.2.

    A1=12.5

    A2=11.2

    d=11.2-12.5=-1.3

    (An)=A1+d(n-1)<0

    подставляем:

    12.5+(-1.3)(n-1)<0

    12.5-1.3n+1.3<0

    13.8<1.3n

    1.3n>13.8

    n>10.6

    т. к. n - всегда целое число, берем только 10, значит, n>10

    A11=A1+10d

    A11=12.5+10*(-1.3)

    A11=12.5+(-13)

    A11=-0.5

    ответ: -0,5

<< < 8910 11 12 > >>