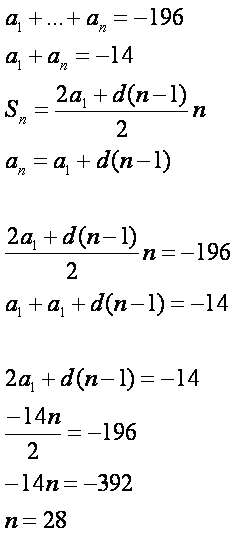найдите n член прогрессии - страница 15
(an) - конечная арифметическая прогрессия, Известно, что a1 +.+an = -196, а a1 + an = -14. Найдите число членов в этой прогрессии?
Решение: 1) Применим формулу суммы n-первых членов арифм. прогрессии:Sn=(a1 + an)*n/2
Подставим в эту формулу данные: -196 = -14*n/2
7*n = 196
n = 196/7 =28
Ответ: в этой прогрессии 28 членов.
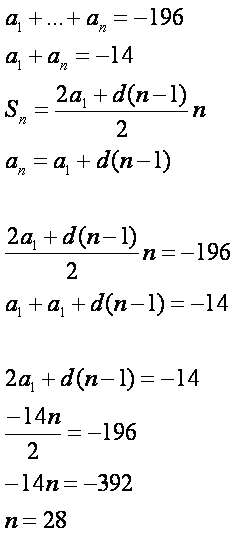
(An)-конечная арифметическая прогрессия. Известно, что а1+.+аn=50, а а1+аn=2,5. Найдите число членов в этой прогрессии
Решение: воспользуемся формулой суммы n первых членовполучим n=40
подробнее во вложениях
ОТВЕТ:40
a1+.an=50
a1+an=2.5
an=a1+(n-1)d
a1+a1+d(n-1)=2.5
2a1+d(n-1)=2.5
S=2a1+d(n-1)/2*n=50
{2a1+d(n-1)=2.5
{n(2a1+d(n-1))=100
{ поделем n=100/2.5=40
1) является ли членом арифметической прогрессии число 143, если a3=13, a16=78
2) найдите первый отрицательный член арифметической прогрессии 32; 27.
3) сколько положительных членов в арифметической прогрессии 23,7 ; 21 ;.
Решение: Составим систему
а₁+15d=78
a₁+2d=13 из первого уравнения вычитаем 2
13d=65, следовательно d=5 подставим в уравнение (2) найдём а₁+10=13, а₁=3
Составим уравнение 143= а₁ +d(n-1)
143=3 + 5n-5, найдём 5n =143+2, n=145:5, n=29,143 является 29 членом прогрессии
2. найдём d=a₂-a₁=27-32=-5
составим неравенство a₁+d(n-1)∠0, решаем 32-5n+5∠0,5n∠-37 домножим всё -1 при этом все знаки меняем 5n больше 37 следовательно n, больше 7,4. Значит n =8, a₈=32-5*7=-3
3. d= 21-23,7=-2,7
составим уравнение a₁+d(n-1) больше 0, получаем 23,7-2,7n+2,7 больше 0,2,7n больше -26,4 домножим всё на-1, меняем знаки
2,7n∠26,4
n∠9,777.
n=9, всего 9является ли число 6,5 членом арифметической прогрессии Аn в которой а1=-2,25 и А11=10,25? Найдите сумму всех натуральных чисел кратных 9 и не превосходящих 80. заранее спасибо
Решение: 1) Найдем разность, через формулу n-го члена.
$$ a_n = a_1+ d(n - 1) $$$$ 10,25=-2,25+d(11-1) $$
$$ d=1,25 $$
По этой же формуле провярем, является ли 6,5 членом арифметической прогрессии. Находим n. Помним, что n - положительное, целое число!$$ 6,5= -2,25 +1.25(n-1) $$
$$ n=6. $$
Следовательно, да, эо число - есть член арифметической прогрессии.2) $$ a_1=9; d=9 $$
Найдем ближайший номер члена арифметической прогрессии не превышающий 80.
$$ 80=9+9(n-1) $$
$$ n=8,8 $$
Ближайший член, номер 8.
$$ S_n=\frac{2a_1+d(n-1)}{2}n $$$$ S_n= \frac{2*9+9(8-1)}{2}8 $$
$$ S_n=324. $$
Ответ: $$ S_n=324. $$
1. Является ли число 35,8 членом арифметической прогрессии, в которой а1=-23,6 и а21=11
2. Найдите номер члена арифметической прогрессии равного 53, если а1=-4; d=3
Решение: 1/Да это сотый элемент а100.
Надо решить два уровнения. Первое находим шаг -23,6+21x=11 Шаг равен 0,6. Дале находим является ли. Если решение следующего уровнения целое число, то является и его номер в прогрессии y+1.
Решаем Уровнение -23,6+у*0,6=35,8. У=99. То есть это сотый элемент.