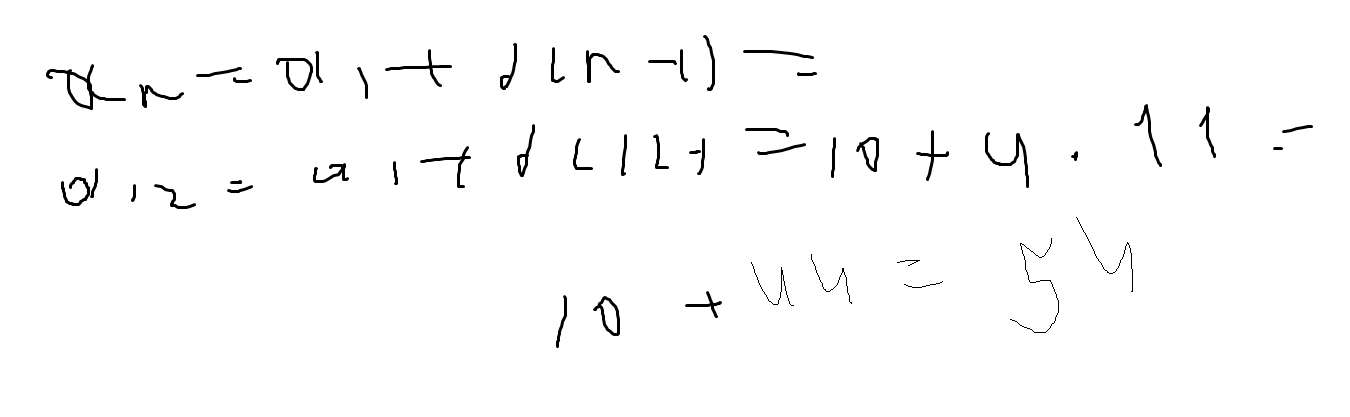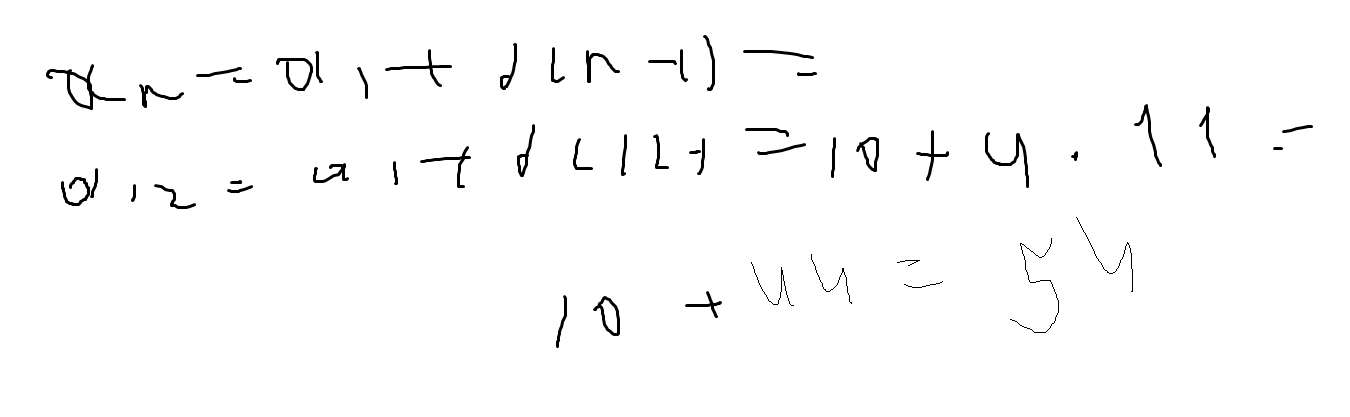найдите n член прогрессии - страница 17
Пусть в арифметической прогрессии третий и десятый члены равны соответственно 12 и (-2). Найдите сумму второго и седьмого членов прогрессии.
Решение: An - арифметическая прогрессияA3 = 12
A10 = -2
Находим d(разность членов прогрессии)
d = (12+2)/(10-3) = 2
A2 = A3 + d = 12+2= 14
A7 = A10+3d = -2-6 = 4
A2 + A7 = 14 + 4 = 18
a3=12 a10=(-2) Найти а2-
а7-Находим d разность арифметической прогрессии
d=(12+2)/7=2а3= a2+d
выражаем a2=a3+d===> a2=12+2=14
a10=a7+3d
выражаем а7=a10+3d===> a7=-2-6 =4a2+a7 = 14+4=18
А) Найдите сумму всех отрицательных членов арифметической прогрессии -7;1; -6,3;.
В) Найдите сумму всех положительных членов арифметической прогрессии 6,3;5,8;.
Решение: A)d=а (2)-а (1)=-6,3-(-7,1)=-6,3+7,1=0,8
а (n)=а (1)+d*(n-1)= -7,1+0,8(n-1)=-7,1+0,8n-0,8=-7,9+0,8n
-7,9+0,8n<0
0,8n<7,9
n<7,9/0,8=79/8=9,125
n<9,125
Значит, n=9, т. к. n- число натуральное.
a(9)=-7,1+0,8*8=-7,1+6,4=-0,7
S(9)=(a(1)+a(n))*n/2= (-7,1-0,9)*10/2=-8*5=-40
Ответ: -40
B) сначала находим разность
d=a2-a1=5,8-6,3=-0,5
значит всего положительных членов 13
S=*n = *13
получаем ответ 42,9Найдите последний член и сумму членов арифметической прогрессии, для которой: d= -11 a16=-15 n=20
Решение: An=A1+d(n-1) составим уравнение :-15=A1-11(16-1)
-15=A1-165
A1=150
далее найдем 20 член т. е. последний(по условию)
An=A1+d(n-1) ; A20= 150-11(20-1)
A20=-59
далее, найдем сумму всех 20 членов по формуле : Sn=(A1+An)n/2 = (150-59)20/2=910
Найдите первый член арифметической прогрессии a(n) если а(4)=4; а(12)=36.
Решение: а(1)- а(4)=4, а(12)=36, Составим систему уравнений с двумя переменными а(1) и d:Система:
а(4)=а(1)+3d
a(12)=a(1)+11d
Выразим в первом уравнении а(1) и подставим во второе:
a(1)=a(4)-3d
a(12)=a(4)-3d+11d Подставим все известные числа, получим:
36=4+8d
8d=32
d=4
Подставляем это значение в первое уравнение:
a(1)=4-3*4=4-12=-8
Ответ : а(1)=-8
Найдите последний член арифметической прогрессии, если известно что а1 равно 10, d равно 4, n равно 11.
Решение: 11=10+4*(n-1)4*(n-1)=11-10=1
n-1=1:4=0.25
n=0.25+1=1.25
Найдите последний член арифметической прогресси если известно что а1 равно 10, d равно 4, n равно 11. это алгебр