- Алгебраическое уравнение n-й степениНаиболее полно элементарная математика рассматривает алгебраические уравнения только двух степеней: первой и второй. Эти уравнения имеют вид: ах + b = 0 (а \(\neq\) 0) ax2 + bx + c = 0 (а \(\neq\) 0). В области комплексных чисел любое алгебраическое уравнение 1-й степени имеет ровно один корень, а любое алгебраическое уравнение 2-й степени - ровно два корня. В высшей алгебрe изучаются...
- Алгоритм исследования свойств квадратичной функцииОбласть определения. Область значений. Четность/нечетность функции. при b = 0 функция четная (то есть \(у = ах^2 +nс= а(-х)^2 + с\); при \(b \neq 0\), функция ни четная, ни нечетная. Нули функции. Если D > 0, то график квадратичной функции имеет два нуля: \(х_1 = \frac{-b -\sqrt{D}}{2a}; x_2 = \frac{-b +\sqrt{D}}{2a}\) и график функции пересекает ось х в 2-х точках. Если D = 0,...
- Арифметическая прогрессияЧисловая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом, называется арифметической прогрессией. Примером арифметической прогрессии является натуральный ряд чисел 1, 2, 3, ... . Каждое его число, начиная со второго, равно предыдущему, сложенному с единицей. Другим примером арифметической прогрессии может служить последовательность 3; 1,5; 0; -1,5; -3..... Каждый член этой последовательности, начиная со второго,...
- Биквадратные уравнения и их решениеБиквадратными называются уравнения вида ax4 + bx2 + c = 0 (1) где a, b и с - заданные числа, причем а \(\neq\) 0. Решение таких уравнений сводится к решению квадратных уравнений. Действительно, полагая в (1) у = x2, получаем: ау2 + by + с = 0. Найдя из этого уравнения у и учитывая, что у = x2, легко получить и х. Пример. Решить уравнение x4...
- Возникновение комплексных чиселВведение комплексных чисел было связано с открытием решения кубического уравнения. И до этого открытия при решении квадратного уравнения \(x^2 + q = px\) приходилось сталкиваться со случаем, когда требовалось извлечь квадратный корень из \((\frac{p}{2})^2 - q\), где величина \((\frac{p}{2})^2\) была меньше чем q. Но в таком случае считалось, что уравнение не имеет решений. О введении новых (комплексных) чисел в то время...
- Возникновение первых математических понятий и методовПроцесс формирования математических понятий и регулярных приемов решения определенных классов элементарных задач охватывает огромный промежуток времени. Его начало, по всей вероятности, относится к далекому времени, когда человек перешел к использованию орудий для добывания средств существования, а затем и к обмену продуктов труда. Завершается этот период с появлением качественно новых форм математического мышления, т. е. тогда, когда совокупность этих понятий и...
- Геометрическая прогрессияФормула общего члена геометрической прогрессии Геометрической прогрессией называется такая числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на некоторое постоянное для данной последовательности число, отличное от нуля. Примеры геометрической прогрессии: 1, 1/3 , 1/9 , 1/27 , ... , 2, 8, 32, 128 , ... , 12, - 6, 3, - 3/2, ....., 1/5 , - 2/5 , 4/5 ,...
- График квадратной функции
 Покажем, как строится график квадратной функции у = ax2 + bx + c. Наше рассмотрение придется разбить на ряд отдельных этапов.
1. График функции у = x2.
Этот график строится «по точкам». Составим следующую таблицу значений функции:
x
-3
-2
-1
-1/2
0
1/2
1
2
3
...
\(y=x^2\)
9
4
1
1/4
0
1/4
1
4
9
...
Отметим соответствующие точки на плоскости координат и соединим их плавной кривой (рис.). Эта кривая называется параболой.На рисунке парабола у = x2 начерчена лишь при -3...
Покажем, как строится график квадратной функции у = ax2 + bx + c. Наше рассмотрение придется разбить на ряд отдельных этапов.
1. График функции у = x2.
Этот график строится «по точкам». Составим следующую таблицу значений функции:
x
-3
-2
-1
-1/2
0
1/2
1
2
3
...
\(y=x^2\)
9
4
1
1/4
0
1/4
1
4
9
...
Отметим соответствующие точки на плоскости координат и соединим их плавной кривой (рис.). Эта кривая называется параболой.На рисунке парабола у = x2 начерчена лишь при -3... - График логарифмической функции
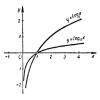 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение... - Графический способ решения систем линейных уравнений
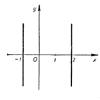 Предположим, что в каждом уравнении системы
$$ \begin{cases}a_1x + b_1y = c_1\\a_2x + b_2y = c_2\end{cases} \;\;\;\;(1) $$
хотя бы один из коэффициентов при неизвестных х и у отличен от нуля. Тогда любое из этих двух уравнений можно рассматривать как уравнение прямой в прямоугольной системе координат.
Действительно, возьмем, например, первое уравнение
a1x + b1y = c1.
Если b1 =/= 0, то уравнение...
Предположим, что в каждом уравнении системы
$$ \begin{cases}a_1x + b_1y = c_1\\a_2x + b_2y = c_2\end{cases} \;\;\;\;(1) $$
хотя бы один из коэффициентов при неизвестных х и у отличен от нуля. Тогда любое из этих двух уравнений можно рассматривать как уравнение прямой в прямоугольной системе координат.
Действительно, возьмем, например, первое уравнение
a1x + b1y = c1.
Если b1 =/= 0, то уравнение...

 Покажем, как строится график квадратной функции у = ax2 + bx + c. Наше рассмотрение придется разбить на ряд отдельных этапов.
1. График функции у = x2.
Этот график строится «по точкам». Составим следующую таблицу значений функции:
x
-3
-2
-1
-1/2
0
1/2
1
2
3
...
\(y=x^2\)
9
4
1
1/4
0
1/4
1
4
9
...
Отметим соответствующие точки на плоскости координат и соединим их плавной кривой (рис.). Эта кривая называется параболой.На рисунке парабола у = x2 начерчена лишь при -3...
Покажем, как строится график квадратной функции у = ax2 + bx + c. Наше рассмотрение придется разбить на ряд отдельных этапов.
1. График функции у = x2.
Этот график строится «по точкам». Составим следующую таблицу значений функции:
x
-3
-2
-1
-1/2
0
1/2
1
2
3
...
\(y=x^2\)
9
4
1
1/4
0
1/4
1
4
9
...
Отметим соответствующие точки на плоскости координат и соединим их плавной кривой (рис.). Эта кривая называется параболой.На рисунке парабола у = x2 начерчена лишь при -3... Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение... Предположим, что в каждом уравнении системы
$$ \begin{cases}a_1x + b_1y = c_1\\a_2x + b_2y = c_2\end{cases} \;\;\;\;(1) $$
хотя бы один из коэффициентов при неизвестных х и у отличен от нуля. Тогда любое из этих двух уравнений можно рассматривать как уравнение прямой в прямоугольной системе координат.
Действительно, возьмем, например, первое уравнение
a1x + b1y = c1.
Если b1 =/= 0, то уравнение...
Предположим, что в каждом уравнении системы
$$ \begin{cases}a_1x + b_1y = c_1\\a_2x + b_2y = c_2\end{cases} \;\;\;\;(1) $$
хотя бы один из коэффициентов при неизвестных х и у отличен от нуля. Тогда любое из этих двух уравнений можно рассматривать как уравнение прямой в прямоугольной системе координат.
Действительно, возьмем, например, первое уравнение
a1x + b1y = c1.
Если b1 =/= 0, то уравнение...