- Квадратные неравенства
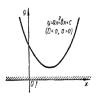Неравенства вида ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c > 0, ax2 + bx + c < 0, где a, b и с - заданные числа и а \(\neq\) 0, называются квадратными (или неравенствами второй степени).
В этом параграфе мы ограничимся лишь рассмотрением неравенств вида
ax2 + bx + c... - Квадратные уравненияУравнение вида $$ ax^2 + bx + c = 0$$ где, a, b, c - действительные числа, причем \(a \neq 0\), называют квадратным уравнением. Если a = 1 , то квадратное уравнение называют приведенным; если \(a \neq 1\), - то неприведенным. Числа a, b, c носят следующие названия a - первый коэффициент, b - второй коэффициент, c...
- Квадратный трехчленУравнения вида ax2 + bx + c = 0, (1) где х - неизвестная величина, а, b, с - данные числа (а \(\neq\) 0), называются квадратными. Выделяя в левой части квадратного уравнения полный квадрат, получаем: $$ a(x+\frac{b}{2a})^2 - \frac{b^2 - 4ac}{4a} = 0 $$ или $$ a(x+\frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2} \;\;\; (2)$$ Очевидно, что уравнение (2) эквивалентно уравнению (1). Уравнение (2) может иметь действительные...
- Комплексные числа: сложение и вычитание
Сумма векторов представляет собой замыкающую многоугольника, составленного из слагаемых векторов. Принимая во внимание, что проекция замыкающей равна сумме проекций составляющих, мы приходим к следующему определению сложения комплексных чисел:
( a1+b1i ) + ( a2+b2i ) + ... + ( an+bni ) =
= ( a1+a2+ ... +an ) + ( b1+b2+ ... +bn )i.
Нетрудно видеть, что сумма комплексных чисел не зависит... - Линейное уравнение с одной переменнойПрактика часто ставит перед нами задачу выяснить, при каких допустимых значениях буквы (или нескольких букв) обе части того или иного равенства принимают одинаковые числовые значения. На равенство в этом случае мы смотрим как на уравнение относительно указанной неизвестной величины. Так, если равенство, а + 4 = 5 (1) рассматривать как уравнение относительно величины а, то легко сообразить, что обе его части принимают...
- Линейные функции и их графики
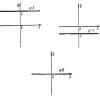Рассмотрим равенство
у = 2х + 1. (1)
Каждому значению буквы х это равенство ставит в соответствие вполне определенное значение буквы у. Если, например, x = 0, то у = 2 • 0 + 1 = 1; если х = 10, то у = 2 • 10 + 1 = 21; при х = - 1/2 имеем у = 2 •... - Математика в Индии
В древней и средневековой математике народов Индии много общего с китайской математикой. В Индии математика тоже является очень древней наукой, издавна составляющей часть культуры. В ней тоже преобладали вычислительно-алгоритмические методы и отсутствовали попытки построения дедуктивных систем; геометрия индийцев — также практическая.
Эта общность характера науки и путей ее развития не случайна и отражает сходность путей исторического развития обеих великих стран и... - Математика древнего Вавилона
Математическое наследие древнего Вавилона. Это название обычно распространяется на совокупность государств, располагавшихся в междуречье Тигра и Евфрата и существовавших в период от 2000 до 200 г. до н. э. До нас дошло около ста тысяч глиняных табличек с клинописными записями. Однако табличек с текстами математического содержания известно только около 50, а математических таблиц без текста — около 200.
Вавилонская система математических... - Математика древнего ЕгиптаНаши познания о древнеегипетской математике основаны главным образом на двух больших папирусах математического характера и на нескольких небольших отрывках. Один из больших папирусов называется математическим папирусом Ринда (по имени обнаружившего его ученого) и находится в Лондоне. Он приблизительно 5,5 м длины и 0,32 м ширины. Другой большой папиpyc, почти такой же длины и 8 см ширины, находится в Москве. Содержащиеся...
- Математика древнего КитаяРазвитие научных знаний в Китае имеет многовековую богатую историю; установлено также и раннее оригинальное развитие китайской математики. Однако до сих пор не преодолена разрозненность и скудность достоверной научной информации о математических познаниях китайцев в древности. По утверждению китайского историка математика Ли Яня, математические познания китайцев восходят к XIV в. до н. э. В истории математики древнего Китая имеются сведения о десятичной...
Неравенства вида ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c > 0, ax2 + bx + c < 0, где a, b и с - заданные числа и а \(\neq\) 0, называются квадратными (или неравенствами второй степени).
В этом параграфе мы ограничимся лишь рассмотрением неравенств вида
ax2 + bx + c...
Сумма векторов представляет собой замыкающую многоугольника, составленного из слагаемых векторов. Принимая во внимание, что проекция замыкающей равна сумме проекций составляющих, мы приходим к следующему определению сложения комплексных чисел:
( a1+b1i ) + ( a2+b2i ) + ... + ( an+bni ) =
= ( a1+a2+ ... +an ) + ( b1+b2+ ... +bn )i.
Нетрудно видеть, что сумма комплексных чисел не зависит...
Рассмотрим равенство
у = 2х + 1. (1)
Каждому значению буквы х это равенство ставит в соответствие вполне определенное значение буквы у. Если, например, x = 0, то у = 2 • 0 + 1 = 1; если х = 10, то у = 2 • 10 + 1 = 21; при х = - 1/2 имеем у = 2 •...
В древней и средневековой математике народов Индии много общего с китайской математикой. В Индии математика тоже является очень древней наукой, издавна составляющей часть культуры. В ней тоже преобладали вычислительно-алгоритмические методы и отсутствовали попытки построения дедуктивных систем; геометрия индийцев — также практическая.
Эта общность характера науки и путей ее развития не случайна и отражает сходность путей исторического развития обеих великих стран и...
Математическое наследие древнего Вавилона. Это название обычно распространяется на совокупность государств, располагавшихся в междуречье Тигра и Евфрата и существовавших в период от 2000 до 200 г. до н. э. До нас дошло около ста тысяч глиняных табличек с клинописными записями. Однако табличек с текстами математического содержания известно только около 50, а математических таблиц без текста — около 200.
Вавилонская система математических...