- Сложение, вычитание, деление десятичных дробей
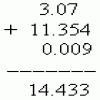Сложение и вычитание десятичных дробей
Эти операции выполняются так же, как и сложение и вычитание целых чисел. Необходимо только записать соответствующие
десятичные знаки один под другим.
Пример:
Сложение и вычитание в столбик
Умножение десятичных дробей
Умножение десятичных дробей производится так же, как и умножение натуральных чисел, по тем же правилам, но в произведении ставится запятая по сумме разрядов множителей в дробной части, считая справа налево (сумма... - Сокращение дробей и приведение их к общему знаменателю
Основное свойство дроби
Так как дробь есть частное от деления числителя на знаменатель, а частное не изменяется от умножения (или деления) делимого и делителя на одно и то же число (кроме нуля), то это же свойство принадлежит и дроби, т. е. величина дроби не изменяется, если её числитель и знаменатель умножить (или разделить) на одно и то же число (кроме нуля).... - Составление уравнения c одним неизвестнымВсякая арифметическая задача состоит в том, что по нескольким известным величинам и по данным соотношениям между этими известными величинами и другими, неизвестными, отыскиваются неизвестные. Алгебра дает особый способ для решения арифметических задач. Этот способ основан на том, что словесно выраженные условия арифметических задач могут быть переведены на математический язык, т.е. выражены посредством алгебраических формул. Перевод словесно выраженных условий задачи на...
- Способы решения алгебраических неравенств
К алгебраическим неравенствам относят:
линейные неравенства;
квадратные неравенства;
рациональные и дробно-рациональные неравенства;
иррациональные неравенства;
показательные и логарифмические, сводящиеся к алгебраическим.
Для решения неравенств используют разные методы, например, графический и аналитический методы, метод равносильных преобразований на основе свойств числовых функций. Достаточно универсальным методом решения неравенств является метод интервалов, поскольку его можно применять для целого класса неравенств.
Метод интервалов
Методом интервалов решают неравенства, приведенные к виду F(x)>0 или F(x)... - Сравнение степенейТеорема 1. Из двух степеней с одинаковыми показателями и положительными основаниями больше та, основание которой больше. Другими словами, если а > b > 0, то при любом натуральном n аn > bn. Это свойство было доказано в разделе про неравенства. Пример. Какое число больше: 2300 или 3200 ? Для решения этой задачи представим данные числа в виде степеней с одинаковыми показателями, используя тождество аmn...
- Среднее арифметическое и среднее геометрическое
Средним арифметическим любых n чисел a1, a2, ... , an называется число
$$ \frac{a_1 + a_2 + ... + a_n}{n} $$
Средним геометрическим n положительных чисел a1, a2, ... , an называется число
$$ \sqrt[n]{a_1 \cdot a_2\cdot ... a_n} $$
Например, для чисел 2 и 8 средним арифметическим будет число \(\frac{2+8}{2}=5\), а средним геометрическим — число \(\sqrt{2\cdot 8} = 4\). Среднее арифметическое чисел 10,... - Тождественные выражения. Тождественное преобразованиеТождественными выражениями называют алгебраические выражения, которые при любых значениях входящих в них переменных приобретают одинаковое значение. Например, тождественны выражения \(x\cdot x\) и \(x^2\), т. к. они равны между собой при любых значениях x. Соответственно, тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных: \(x\cdot x = x^2\). Когда надо подчеркнуть тождественность выражений в отличие от их равенства, используется математический знак "тождественно равно": ≡. Запись f(x) = g(x)+1 может рассматриваться...
- Точки в системе координат
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... - Тригонометрическая форма комплексных чисел
Вместо того, чтобы определить вектор \(\overrightarrow{MN}\) его проекциями a и b на координатные оси, мы можем определить его двумя другими величинами, а именно: его длиной r и углом φ, который направление \(\overrightarrow{MN}\) образует с положительным направлением оси OX. Если же мы считаем, что комплексное число a + bi соответствует точке с координатами ( a, b ), то r и φ... - Умножение многочленов
Умножение степеней одного и того же числа
Пусть надо умножить а3 на а2, что можно обозначить так: а3а2, или подробнее: (ааа) (аа). Здесь произведение ааа умножается на другое произведение аа. Но чтобы умножить какое-нибудь число на произведение, можно умножить это число на первый сомножитель, полученный результат умножить на второй сомножитель, и т. д.; поэтому:
а3а2 = (ааа)(аа) = (ааа) аа,
что может...
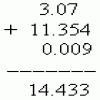Сложение и вычитание десятичных дробей
Эти операции выполняются так же, как и сложение и вычитание целых чисел. Необходимо только записать соответствующие
десятичные знаки один под другим.
Пример:
Сложение и вычитание в столбик
Умножение десятичных дробей
Умножение десятичных дробей производится так же, как и умножение натуральных чисел, по тем же правилам, но в произведении ставится запятая по сумме разрядов множителей в дробной части, считая справа налево (сумма...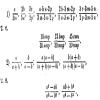
Основное свойство дроби
Так как дробь есть частное от деления числителя на знаменатель, а частное не изменяется от умножения (или деления) делимого и делителя на одно и то же число (кроме нуля), то это же свойство принадлежит и дроби, т. е. величина дроби не изменяется, если её числитель и знаменатель умножить (или разделить) на одно и то же число (кроме нуля)....
К алгебраическим неравенствам относят:
линейные неравенства;
квадратные неравенства;
рациональные и дробно-рациональные неравенства;
иррациональные неравенства;
показательные и логарифмические, сводящиеся к алгебраическим.
Для решения неравенств используют разные методы, например, графический и аналитический методы, метод равносильных преобразований на основе свойств числовых функций. Достаточно универсальным методом решения неравенств является метод интервалов, поскольку его можно применять для целого класса неравенств.
Метод интервалов
Методом интервалов решают неравенства, приведенные к виду F(x)>0 или F(x)...
Средним арифметическим любых n чисел a1, a2, ... , an называется число
$$ \frac{a_1 + a_2 + ... + a_n}{n} $$
Средним геометрическим n положительных чисел a1, a2, ... , an называется число
$$ \sqrt[n]{a_1 \cdot a_2\cdot ... a_n} $$
Например, для чисел 2 и 8 средним арифметическим будет число \(\frac{2+8}{2}=5\), а средним геометрическим — число \(\sqrt{2\cdot 8} = 4\). Среднее арифметическое чисел 10,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Вместо того, чтобы определить вектор \(\overrightarrow{MN}\) его проекциями a и b на координатные оси, мы можем определить его двумя другими величинами, а именно: его длиной r и углом φ, который направление \(\overrightarrow{MN}\) образует с положительным направлением оси OX. Если же мы считаем, что комплексное число a + bi соответствует точке с координатами ( a, b ), то r и φ...
Умножение степеней одного и того же числа
Пусть надо умножить а3 на а2, что можно обозначить так: а3а2, или подробнее: (ааа) (аа). Здесь произведение ааа умножается на другое произведение аа. Но чтобы умножить какое-нибудь число на произведение, можно умножить это число на первый сомножитель, полученный результат умножить на второй сомножитель, и т. д.; поэтому:
а3а2 = (ааа)(аа) = (ааа) аа,
что может...