- Пропорциональная зависимость (прямая и обратная)Пропорциональная зависимость Каждый из опыта знает, что если объем воды увеличится (или уменьшится) в каком-нибудь отношении, то и вес ее увеличится (или уменьшится) в том же отношении. например, 1 л воды весит 1 кг, 2 л воды весят 2 кг, 21/2 л воды весят 21/2 кг и т. д. (предполагается, конечно, что все прочие условия, влияющие на вес воды, остаются неизменными;...
- Разложение алгебраических выражений на множителиГоворя об алгебраическом делении, мы указывали, что в некоторых случаях частное можно только обозначить знаком деления. Получаемые при этом выражения, вроде таких: $$ \frac{a}{b}, \frac{2x}{3a}, \frac{x^2-4x+y^2}{x+y} $$ принято называть алгебраическими дробями по сходству этих выражений с арифметическими дробями. Алгебраические дроби, подобно арифметическим, могут быть иногда упрощены посредством сокращения (т.е. посредством деления) делимого и делителя на их общие множители, если таковые окажутся. Для того,...
- Разложение на простые множителиСначала разберемся с тем, что такое простые множители. Понятно, раз в этом словосочетании присутствует слово "множители", то имеет место произведение каких-то чисел, а уточняющее слово "простые" означает, что каждый множитель является простым числом. Например, в произведении вида 2·7·7·23 присутствуют четыре простых множителя: 2, 7, 7 и 23. А что же значит разложить число на простые множители? Это значит, что данное число нужно представить...
- Рациональные числа и действия над ними
Первой математической операцией, с которой столкнулся человек, был счет предметов. В результате счета предметов получаются целые положительные числа, иначе называемые натуральными. Расположенные в порядке возрастания, они образуют натуральный ряд чисел
1, 2, 3, 4.....
После натуральных чисел в математику были введены положительные дроби, то есть числа вида m/n, где m и n - произвольные натуральные числа. Введение этих чисел в математику... - Решение иррациональных уравненийИррациональными уравнениями называются уравнения, содержащие неизвестное под знаком радикала. К таким относятся, например, уравнения \(\sqrt{x - 1}\) = 3 + \(\sqrt{x}\) , \(\sqrt{x}\)= 5 - 4х, \(\sqrt[3]{2-x}\) = \(\sqrt[4]{x+6}\)+7x и т. д. Мы ограничимся рассмотрением иррациональных уравнений, которые содержат только квадратные радикалы. В связи с этим следует напомнить, что квадратные корни можно извлекать только из неотрицательных чисел. Такие, например, выражения, как \(\sqrt{-3}\), \(\sqrt{-25}\),...
- Решение уравнений с модулем методом интервалов
При решении некоторых уравнений, содержащих неизвестное под знаком абсолютной величины, часто используют так называемый метод интервалов. Продемонстрируем этот метод на примере уравнения
|x + 1| + |x - 2| = 3 (1)
Это уравнение содержит две абсолютные величины: | х + 1 | и | х - 2|. Первая из них обращается в нуль при х = - 1,... - Свойства десятичных логарифмовЗа основание логарифмов часто принимают число 10. Логарифмы чисел по основанию 10 называются десятичными. Для обозначения десятичных логарифмов обычно используют знак lg, а не log; при этом число 10, указывающее основание, не пишут. Например, вместо log10105 пишут просто: lg 105; вместо log102 пишут lg 2 и т. д. Десятичным лосарифмам присущи все те свойства, которыми обладают логарифмы при основании, большем 1....
- Свойства логарифмической функции
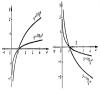Рассмотрим основные свойства логарифмической функции
y = logax (1)
Напомним, что под а в формуле (1) мы подразумеваем любое фиксированное положительное число, отличное от 1.
Свойство 1. Областью определения логарифмической функции служит множество всех положительных чисел.
Действительно, пусть b есть произвольное положительное число. Покажем, что выражение \(\log_a b\) определено. Как мы знаем, \(\log_a b\) есть не что иное, как корень уравнения
аz = b (2)
Если... - Системы линейных неравенств
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >... - Сложение и вычитание дробей с разными знаменателямиЧтобы сложить или вычесть дроби с разными знаменателями сначала их нужно привести к общему знаменателю и только потом выполнять сложение или вычитание числителей Нужно обе дроби привести к одинаковому знаменателю. Для этого нужно подобрать число, наименьший общий множитель, и разделить это число на знаменатель данных дробей. Полученное число нужно написать у дроби (у числителя) как дополнительный множитель. Потом перемножить, записать под...
Первой математической операцией, с которой столкнулся человек, был счет предметов. В результате счета предметов получаются целые положительные числа, иначе называемые натуральными. Расположенные в порядке возрастания, они образуют натуральный ряд чисел
1, 2, 3, 4.....
После натуральных чисел в математику были введены положительные дроби, то есть числа вида m/n, где m и n - произвольные натуральные числа. Введение этих чисел в математику...
При решении некоторых уравнений, содержащих неизвестное под знаком абсолютной величины, часто используют так называемый метод интервалов. Продемонстрируем этот метод на примере уравнения
|x + 1| + |x - 2| = 3 (1)
Это уравнение содержит две абсолютные величины: | х + 1 | и | х - 2|. Первая из них обращается в нуль при х = - 1,...
Рассмотрим основные свойства логарифмической функции
y = logax (1)
Напомним, что под а в формуле (1) мы подразумеваем любое фиксированное положительное число, отличное от 1.
Свойство 1. Областью определения логарифмической функции служит множество всех положительных чисел.
Действительно, пусть b есть произвольное положительное число. Покажем, что выражение \(\log_a b\) определено. Как мы знаем, \(\log_a b\) есть не что иное, как корень уравнения
аz = b (2)
Если...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...