разложите на множители числитель и знаменатель дроби - страница 9
Разложите на множители 2ax+bx-ay-by
В треугольнеке MKE угол M равен 41, угол K52. Вычислите угол E
Один из смежных углов на 48 больше другого, Найдите меньший угол
Треугольник с какими сторонами можно изобразить
а)6;2;3 б)18;11;4 в)15;6;6 г)25;9;17
Решение: 1)
2ax + bx - ay - by = ax + x*(a+b) - y*(a+b) = ax + (a+b)*(x-y)
2) Сумма углов треугольника равна 180.
Угол Е = 180 - 41 - 52 = 87
3) Сумма смежных углов равна 180 градусов.
(180 - 48)/2 = 66 град - первый угол
66+48 = 114 град - смежный ему.
4) Сумма двух сторон должна быть больше третьей стороны.
а) 2+3=5 <6 - нельзя
б) 11+4 = 15< 18 - нельзя
в) 6+6=12 <15 - нельзя
г - можно - 9+17 = 26> 251) выделите квадрат суммы или разности из квадратного трехчлена:
а) х^2+10x-20;
б)x^2-6х+15;
в)x^2-5x-4;
г)x^2+x+1;
2) выделите квадрат двучлена из неполного квадратного трехчлена:
а)x^2+7x;
б)x^2-x;
3) разложите на множители квадратный трехчлен:
а)x^2-х-6;
б)x^2+3x-4;
в)x^2-8x+15;
г)x^2+8x+12.
Решение: х^2+2xу+у^2=(х+у)^2 - это формула квадрат суммых^2-2xу+у^2=(х-у)^2 - это квадрат разности
а) х^2+10x-20,
смотрите на средний показатель - 10х, делите его на 2, получили 5х, значит второе значение в скобке (у) будет 5, подставим, получим:
(х+у)^2=х^2+10х+25 - а у нас в выражении -20, тогда от начальной скобки надо отнять 45:
(х+у)^2-45=х^2+10х+25-45=х^2+10x-20
х^2+10x-20=(х+у)^2-45
б)x^2-6х+15=(х-3)^2+6
в)x^2-5x-4=(х-2)^2-x-8
г)x^2+x+1=(х+1)^2-х
1) а) (х²+10х+25)-45=(х+5)²-45. это так что-ли?
б) х²-6х+15=(х²-6х+9)+6=(х-3)²+6.
в) х²-5х-4=(х²-5х+6,25)-10,25=(х-2,5)²-10,25.
г) х²+х+1=(х²+х+1/4)-5/4=(х+1/2)²-5/4.
2) а) х²+7х=(х²+7х+12,25)-12,25=(х+3,5)²-12,25.
б) х²-х=(х²-х+1/4)-1/4=(х-1/2)²-1/4.
3) а) х²-х-6=(х-3)(х+2).
б) х²+3х-4=(х-1)(х+4).
в) х²-8х+15=(х-3)(х-5).
г) х²+8х+12=(х+2)(х+6).
Разность чисел 5632 и 867 равна : 1)4865, 2)5765. 3)4765, 4)3565
Сколько цифр содержит частное 122304 : 48. 1) 5, 2)4, 3) 3, 4) 2
Увеличь число 2603 в 58 раз. 1) 150974, 2) 15974, 3) 1594, 4) 15097
Один из множителей равен 19, значение произведения равно 950. Чему равен другой множитель? 1) 5, 2) 6, 3) 40, 4) 50
В одной коробке 6 карандашей. Сколько нужно коробок чтобы разложить 720 карандашей?
1) 12, 2) 150, 3) 120, 4) 16
За 5 дней Вася прочитал 60 страниц. Сколько нужно коробок, чтобы разложить 720 карандашей?
1) 12, 2) 150, 3) 120, 4) 16
Решение: 5632 - 867 = 4765
Ответ: 3)
122304 : 48 = 2548 - четыре цифры
Ответ: 2)
2603 * 58 = 150974
Ответ: 1)
950 : 19 = 50
Ответ: 4)
720 : 6 = 120 коробок
Ответ: 3)1) 3 (5632-867=4765)
2) 2 (122304:48=2548(ну и посчитать=4))
3) 1 (2603*58=150974)
4) 4 (950:19=50)
5) 3 (720:6=120)
6) 1 (60:5=12)
Разложение на множители \( x^2 -2x-15 \\ x^2-16 \\ x^2-2x+1 \\ 3x^2+8x-3=3\)
Решение: $$ x^2=2x-15=(x-3)(x+5) \\ x^2-16=(x-4)(x+4) \\ x^2-2x+1=(x-1)^2 \\ 3x^2+8x-3=3 \\ 3x^2+8x=x(3x+8) $$
1) х²+2х-15=(х-3)(х+5)
х²+2х-15=0
D=b²-4ac=4+60=64
x1=-b+√D/2a=-2+8/2=6/2=3
x2=-b-√D/2a=-2-8/2=-10/2=-5
2) х²-16=(х-4)(х+4)
3) х²-2х+1=(х-1)²
4) 3х²+8х-3=3(х-1/3)(х+3)
х²+8/3х - 1 = 0
D=b²-4ac=64/9 + 4 = 7 1/9 + 4 = 11 1/9 = 100/9
x1=-b+√D/2a=-8/3 + 10/3 : 2 = 2/3 : 2 = 1/3
х2=-b-√D/2a = -8/3 - 10/3 : 2 = -18/3 : 2 = - 3
Разложение на множители
а) х³-2х=
б)5а²-10аb+5b²
в)cm-cn+3m-3n
Решение: а) х³-2х=x(x²-2)
б)5а²-10аb+5b²=5(a²-2ab+b²)=5(a+b)²
в)cm-cn+3m-3n = c(m-n) + 3(m-n) = (m-n)(c+3)
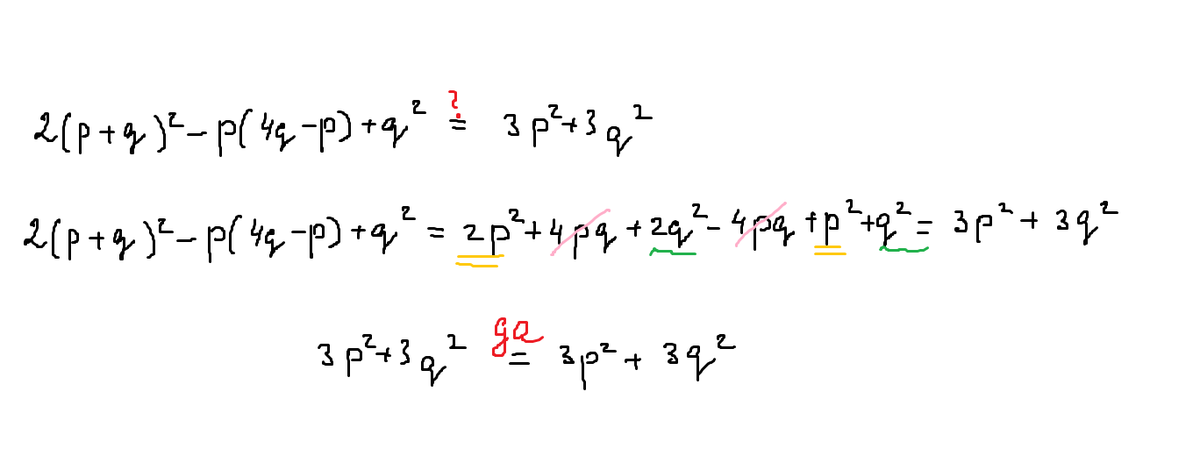

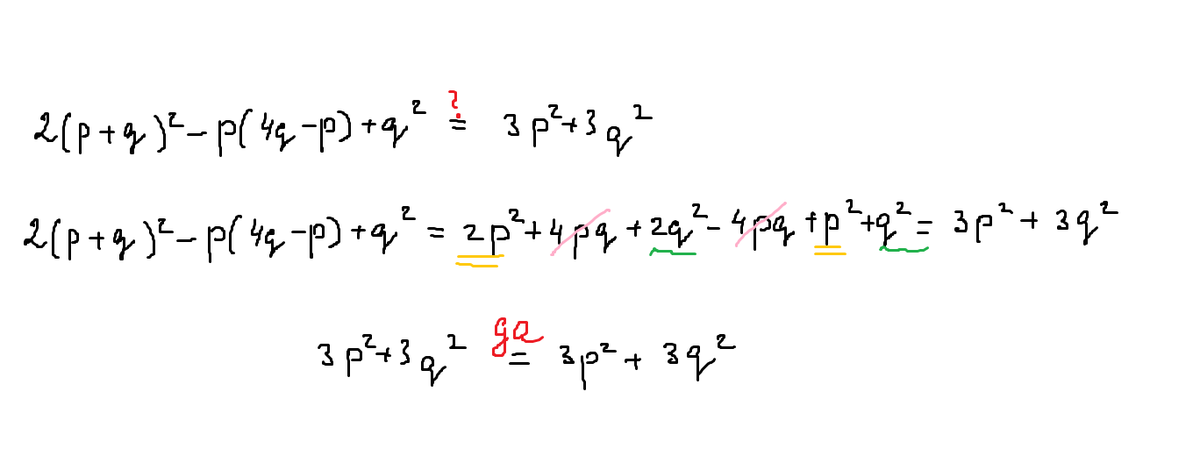
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...