график функции »
график функции пересекает - страница 4
Даны функции: f(x)=x²-2x и g(x)=3x-4. Найдите:
а) f(-2); g(-10); f(g(-1)).
б) Значения x, при которых f(x)=3.
в) Точки пересечения графиков данных функций с осями координат.
г) Координаты точек, в которых пересекаются графики данных функций.
д) Все точки, в которых график функции y=f(x) лежит выше графика функции y=g(x) )) )
Решение: F(x)=x²-2x q(x)=3x-4
a)f(-2)=(-2)²-2*(-2)=4+4=8
б)f(q(x))=(3x-4)²-2(3x-4)=9x²-24x+16-6x+8=9x²-30x+24
f(q(-1))=9*(-1)²-30*(-1)+24=9+30+24=63
в)f(x)=x²-2x
х=0⇒у=0
у=0⇒х²-2х=0⇒х(х-2)=0⇒х=0 и х=2
(0;0),(2;0)
q(x)=3x-4
х=0⇒у=-4
у=0⇒3х-4=0⇒х=1 1/3
(0;-4) и (1 1/3;0)
г)x²-2x =3х-4
х²-5х+4=0
х1+х2=5 и х1*х2=4
х=1 ⇒у=3*1-4=-1и х=4⇒у=3*4-4=8
(1;-1) и (4;8)
д)x²-2x >3х-4
х²-5х+4>0
+ _ +
____________________________
1 4
x∈(-∞;1) (4;∞)
Пересекаются ли графики функции y=1.2x-5, и y=5x-0.8? Если да, то найдите координаты этой точки.
Решение: У=1,2х -5. К1=1,2
У=5х -0,8. К2=5
Угловые коэффициенты не равны, значит прямые пересекутся, а если так то у точки пересечения координаты общие, поэтому можно прировнять у
1.2х-5=5х -0,8
1,2х -5х= 5 -0,8
-3,8х= 4,2
Х= - 21/19
Это координата Х
Найдём у, подставим в любое уравнение
У=1,2*(-21/19) -5=6/5*
(-21/19) -5=
-126/95-5= -6 31/95
А(-21/19; -6 31/95)
Найдите координаты точек, в которых график функции
y=(x-2)^2(2x+3)(3x-4,5)
а) пересекает ось х
б) касается оси х
Решение: (x-2)²(2x+3)(3x-4,5)
а) пересекает ось х
2х+3=0 или 3х-4,5=0
2х=-3 или 3х =4,5
х=-3/2=-1,5 или х=1,5
б) касается оси х в точке х=2
Проходя через эту точку график не переходит из нижней полуплоскости в верхнюю, а остается в верхней полуплоскости и касается оси ох
Не выполняя построения определите пересекаются ли графики функции. Если пересекаются то найдите координаты точек пересечения у=1/3х^2 и у=6х-15
Решение: Составляем систему уравнений.
y = 1/3x^2
y = 6x - 15
Смотри
Дальше получается обычное квадратное уравнение
решаем его
1/3x^2-6x +15 =0
D = 36 - 4*15*1/3 = 36 - 20 = 16
x1 = (6 + 4)/ 2/3 = 15
x2 = 2 / 2/3 = 3
Если х1 = 15, то у1 = 75
Если х2 = 3, тоу2 = 3
Получается, что графики пересекаются в 2 точках (15,75) и (3,3)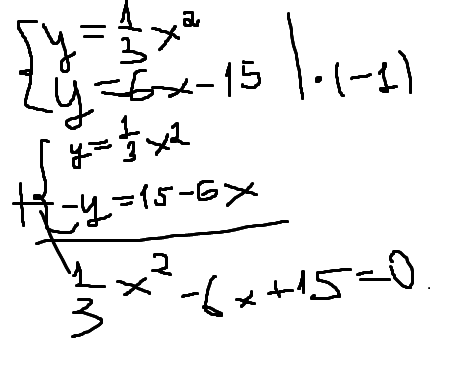
Графики функций у=ax^2 и у=1-2x пересекаются в точке (2; -3). Найдите координаты второй точки пересечения этих графиков
Решение: Найдем a, зная одну из точек пересечения$$ -3 = a2^2 $$
a = -3/4
$$ -3/4x^2 = 1 - 2x $$
Умножим обе части уравнения на 4
$$ -3x^2 + 8x - 4 = 0 $$
Используем теорему Виета
x1 + x2 = -b/a
x1*x2 = c/a
x1 = 2 (известна одна из точек пересечения x = 2)
x1*x2 = 4/3
x2 = 2/3
x = 2/3, находим соответственно y = -1/3
(2/3,1/3)

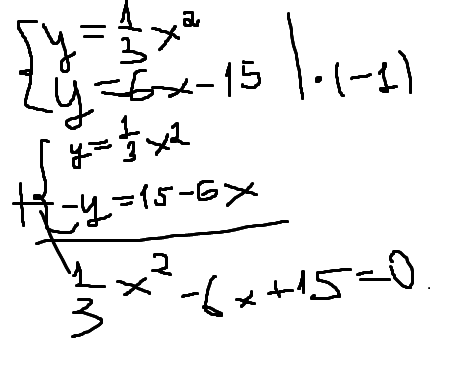
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...