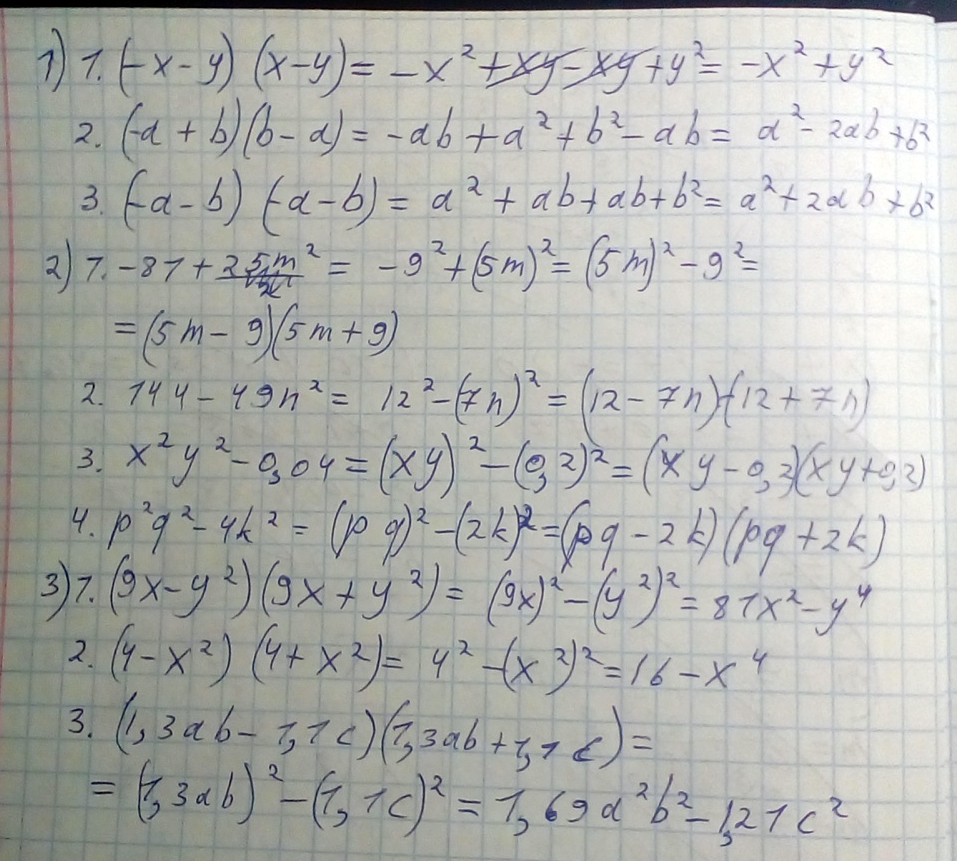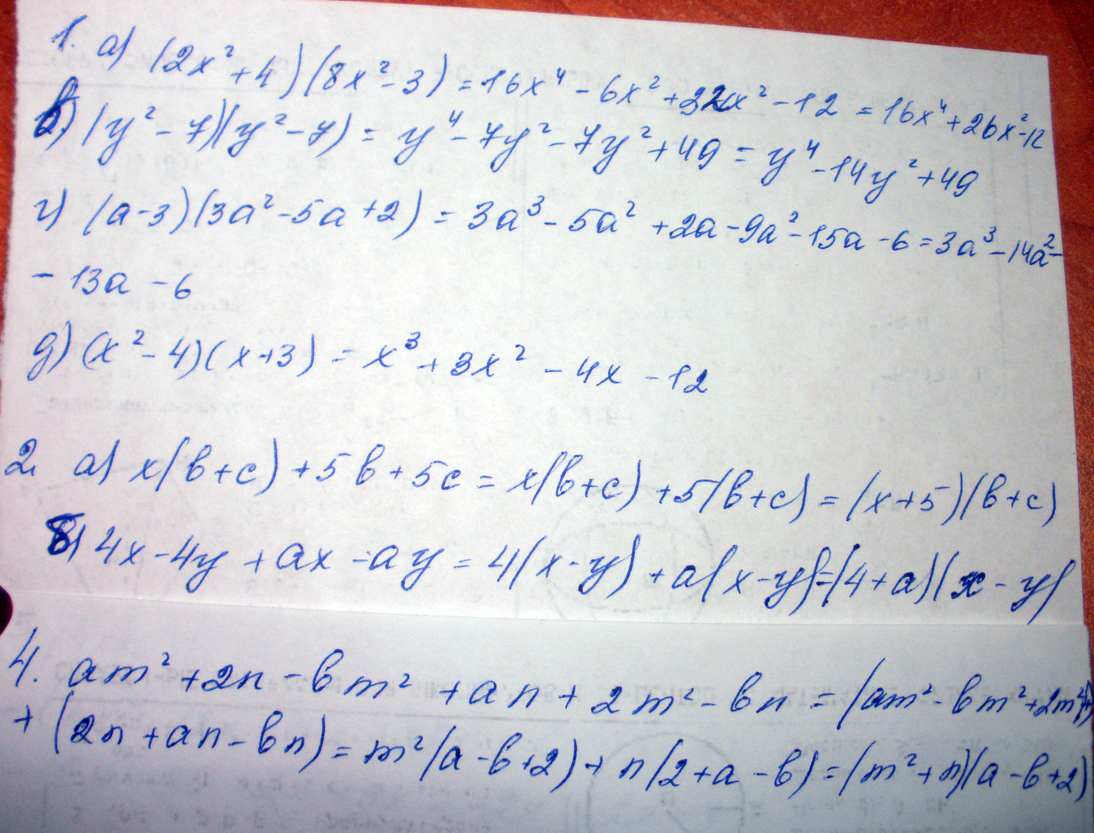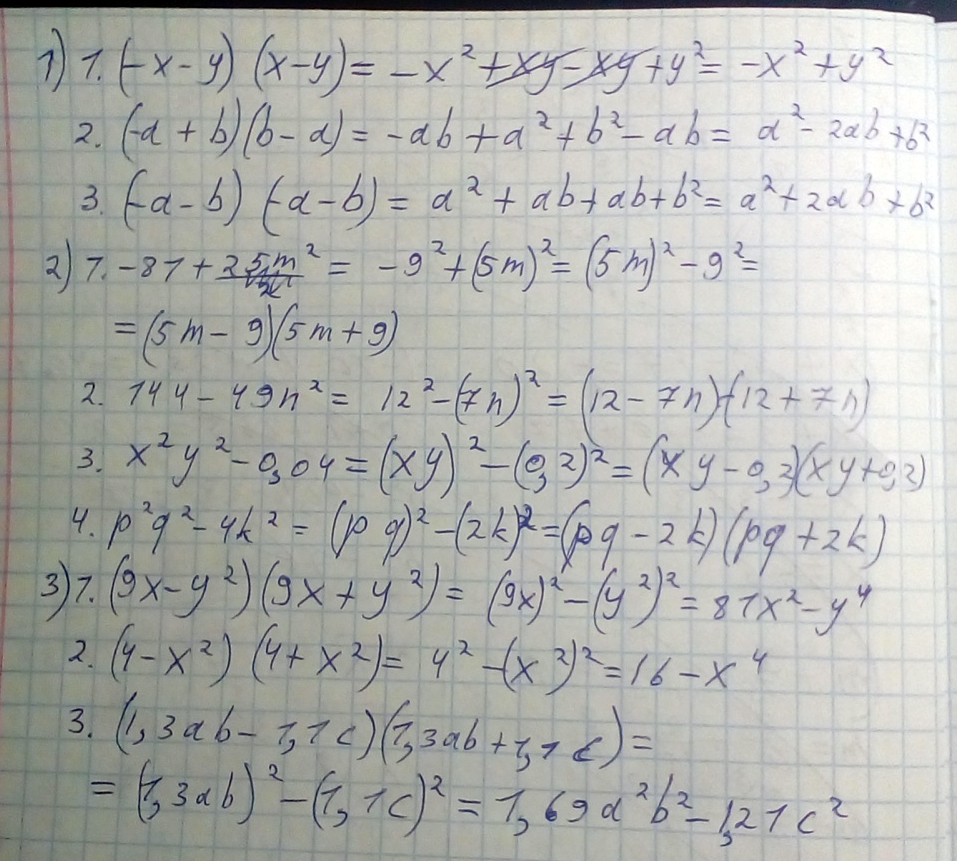представьте в виде многочлена - страница 5
1. Вычислите наиболее рациональным способом:
а) (71)^2
б) 11^2+22*19+19^2
2. Представьте в виде многочлена выражение:
а) (5х+2y)^2+(5x-2y)^2
б) (a+2b)^2-(a+b)^2
3. Разложите на множители
4x^2-4x-4y-y^2-3
Решение: 1. a) (71)^2=(70+1)^2=(70)^2+2*70*1+1^2=4900+140+1=5041б) 11^2+22*19+19^2=11^2+2*11*19+19^2=(11+19)^2=(30)^2=900
2. а) (5х+2y)^2+(5x-2y)^2=25х^2+20xy+4y^2+25x^2-20xy+4y^2=50x^2+8y^2
б) (a+2b)^2-(a+b)^2=a^2+4ab+4b^2-a^2-2ab-b^2=2ab+3b^2
3. 4x^2-4x-4y-y^2-3=(4x^2-4x+1)-(4y+y^2+4)=(2x-1)^2-(y+2)^2=(2x-1+y+2)(2x-1-y-2)=
=(2x+y+1)(2x-y-3)
1. Вычислите наиболее рациональным способом:
a) 71²=(70+1)²=70²+2·70·1+1²=4 900+140+1=5 041
б) 11²+22·19+19²=11²+2·11·19+19²=(11+19)²=30²=900
в обоих случаях использовали формулу сокращённого умножения
(a+b)²=a²+2ab+b²
2. Представьте в виде многочлена выражение:
а) (5х+2y)²+(5x-2y)²=(25х²+20xy+4y²)+(25x²-20xy+4y²)=
25х²+20xy+4y²+25x²-20xy+4y²=(25х²+25x²)+(20xy-20xy)+(4y²+4y²)=50x²+8y²
б) (a+2b)²-(a+b)²=(a²+4ab+4b²)-(а²+2аb+b²)=a²+4ab+4b²-a²-2ab-b²=
(a²-a²)+(4ab-2ab)+(4b²-b²)=2ab+3b²
в обоих случаях использовали формулу сокращённого умножения
(a+b)²=a²+2ab+b²
(a-b)²=a²-2ab+b²
3. Разложите на множители
4x²-4x-4y-y²-3=(4x²-4x+1)-(у²+4y+4)=(2x-1)²-(y+2)²=((2x-1)+(y+2))((2x-1)-(y+2))=
(2x-1+y+2)(2x-1-y-2)=(2x+y+(-1+2))(2x-y+(-1-2))=(2x+y+1)(2x-y-3)
1. Вычислите наиболее рациональным способом:
а) (71)^2
б) 11^2+22*19+19^2
2. Представьте в виде многочлена выражение:
а) (5х+2y)^2+(5x-2y)^2
б) (a+2b)^2-(a+b)^2
3. Разложите на множители
4x^2-4x-4y-y^2-3
Решение: 1. Вычислите наиболее рациональным способом:a) 71²=(70+1)²=70²+2·70·1+1²=4 900+140+1=5 041
б) 11²+22·19+19²=11²+2·11·19+19²=(11+19)²=30²=900
в обоих случаях использовали формулу сокращённого умножения
(a+b)2=a2+2ab+b2
2. Представьте в виде многочлена выражение:
а) (5х+2y)²+(5x-2y)²=(25х²+20xy+4y²)+(25x²-20xy+4y²)=
25х²+20xy+4y²+25x²-20xy+4y²=(25х²+25x²)+(20xy-20xy)+(4y²+4y²)=50x²+8y²
б) (a+2b)²-(a+b)²=(a²+4ab+4b²)-(а²+2аb+b²)=a²+4ab+4b²-a²-2ab-b²=
(a²-a²)+(4ab-2ab)+(4b²-b²)=2ab+3b²
в обоих случаях использовали формулу сокращённого умножения
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
3. Разложите на множители
4x²-4x-4y-y²-3=(4x²-4x+1)-(у²+4y+4)=(2x-1)²-(y+2)²=((2x-1)+(y+2))((2x-1)-(y+2))=
(2x-1+y+2)(2x-1-y-2)=(2x+y+(-1+2))(2x-y+(-1-2))=(2x+y+1)(2x-y-3)
1) Представьте в виде многочлена 0,5y(6-2y^2)(3+y^2)
2) Разложите на множители многочлен 5z+30a+bz+6ba
3) Найдите три последовательный натуральных числа, если произведение двух больших чисел больше произведения двух меньше на 28.
Решение: 1) 0,5у(6-2у²)(3+у²)=0,5у*2*(3-у²)(3+у²)=у*(3² - (y²)²)=y*(9-y⁴)=9y-y⁵
2) 5z+30a+bz+6ba=(5z+bz)+(30a+6ba)=z(5+b)+6a(5+b)=(5+b)(z+6a)
3) n - 1-ое натуральное число
n+1 - 2-ое натуральное число
n+2 - 3-е натуральное число
(n+1)(n+2)-n(n+1)=28
(n+1)(n+2-n)=28
2*(n+1)=28
n+1=28 : 2
n+1=14
n=14-1
n=13 - 1-ое натуральное число
n+1=13+1=14 - 2-ое натуральное число
n+2=13+2=15 - 3-е натуральное число
Ответ: 13; 14; 15.Представьте в виде многочлена выражение:
а) (2х²+4)(8х²-3) в) (у²-7)(у²-7) д) (х²-4)(х+3)
б) (2с²-с+6) г) (а-3)(3а²-5а+2)
Разложите на множители многочлен:
а) х(b+c)+5b+5c
б)4x-4y+ax-ay
Докажите, что значение выражения не зависит от переменной x
(4x+3)(x+4)-(3x+5)(2x+4)+x(2x+3)
Представьте в виде произведения:
am²+2n-bm²+an+2m²-bn
Решение: 1. а)16*x^4+26*x^2-12
б)
в)y^4-14*y^2+49
г)3*a^3-14*a^2+17*a-6
д)x^3+3*x^2-4*x-12
2. а)(c+b)*x+5*c+5*b
(c+b)*(x+5)
б)(-(a+4))*(y-x)
3. В третьем будет -8, а х сократился. Значит доказано что выражение не зависит от переменой.
4.(-b+a+2)*n+(-b+a+4)*m^2
-(b*n-a*n-2*n+b*m^2-a*m^2-4*m^2)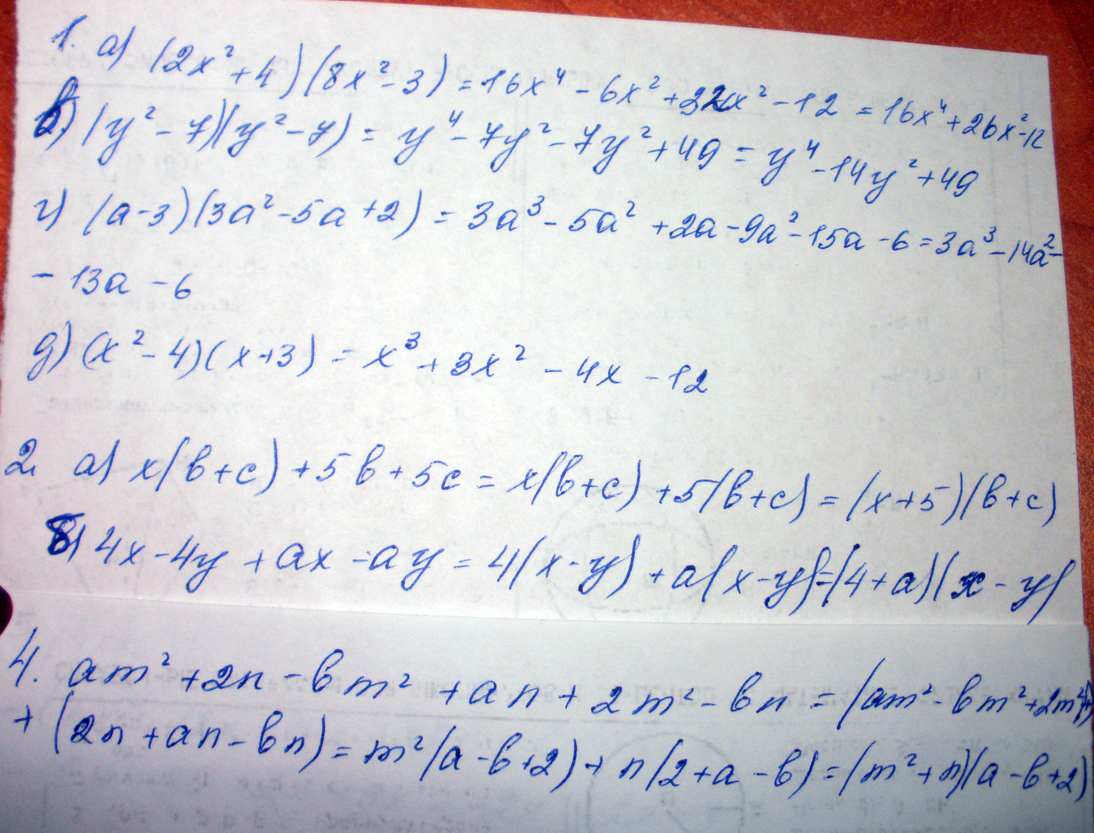
1) Представьте в виде многочлена:
1.(-x-y)(x-y)=
2.(-a+b)(b-a)=
3.(-a-b)(-a-b)=
2. Разложите на многочлены:
1.81+25m\2=
2. 144-49n\2=
3. x\2y\2-0.04=
4. p\2q\2-4k\2=
3. Выполни умножения:
1. (9x-y\2)(9x+y\2)=
2. (4-x\2)(4+x\2)=
3. (1.3ab-1.1c)(1.3ab+1.1c)=
Решение: .
При решении использована формула разности квадратов:
a²-b²=(a-b)*(a+b)
И наоборот:
(a-b)*(a+b)=a²-b²