НОД и НОК »
наибольший общий делитель равен наименьшему общему кратному - страница 6
Наибольший общий делитель чисел 28 и 42
Решение: Ответ 14
28/14=2
42/14=3Наибольший общий делитель или НОД двух чисел — это наибольшее число, на которые исходные числа делятся без остатка. Возьмем два числа — 72 и 64. Найдем делители каждого из этих чисел: делители числа 72 — 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72делители числа 64 — 1, 2, 4, 8, 16, 32, 64
В твоем случае 28-1, 2, 4, 7, 14, 24
72-1, 2, 3, 4, 6, 8, 18.
НОД у 28 и 42 будет 8Наибольший общий делитель 335,315 и 450
Решение: 335 : 5 = 67 315 : 3 = 105 450 : 2 = 225
67 : 67 = 1 105 : 3 = 35 225 : 3 = 75
335 = 5 * 67 35 : 5 = 7 75 : 3 = 25
7 : 7 = 1 25 : 5 = 5
315 = 3 * 3 * 5 * 7 5 : 5 = 1
450 = 2 * 3 * 3 * 5 * 5
НОД (335; 315 и 450) = 5 - наибольший общий делительНОД(Наибольший общий делитель) 144,648,726
Решение: 144 = 2^4 * 3^2
648 = 2^3 * 3^4
726 = 2^1 * 3^1 * 11^2
Значит, НОД(144, 648, 726) = 2^min(4, 3, 1) * 3^min(2, 4, 1) * 11^min(0, 0, 2) = 2 * 3 = 6
Ответ: 6144\2\2\3\3\2\2=1
648\3\3\3\3\2\2\2=1
726\3\2\11\11=1
\=разделить
3*2=6
Ответ: НОД=6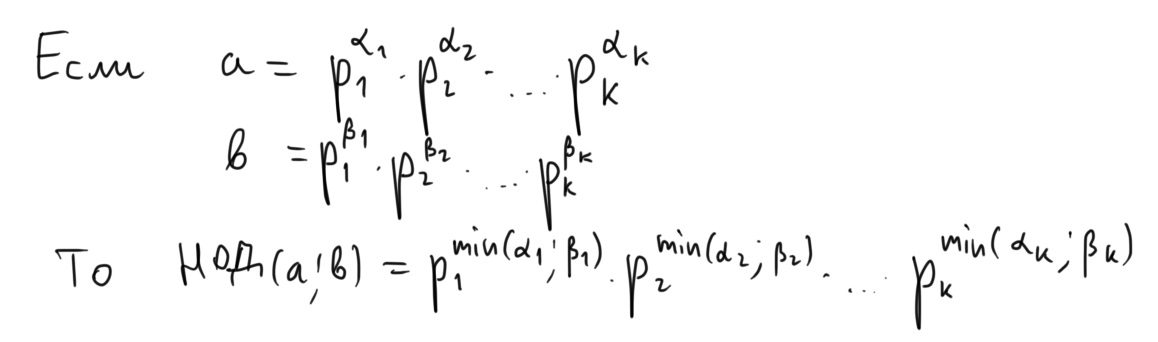
найди наибольший общий делитель методом разложения на простые множители 520и 468 814и 4400
Решение: 520/2=260
260/2=130
130/2=65
65/5=13
13/13=1
2*2*2*5*3=520
468/2=234
234/2=117
117/3=39
39/3=13
13/13=1
2*2*3*3*13=468
Наибольший общий делитель=13
814/2=407
407/11=37
37/37=1
2*11*37=814
4400/2=2200
2200/2=1100
1100/2=550
550/2=275
275/5=55
55/5=11
11/11=1
2*2*2*2*5*5*11=4400
Наибольший общий делитель =11Найдите наибольшие общий делитель чисел способом перебора делителей
12 и 32
30 и 42
35 и 60
Решение: 12 | 2 32 | 2 12 = \( 2^{2}\) * 3
6 | 2 16 | 2 32 =\(2^{5}\)
3 | 3 8 | 2 НОД ( 12; 32 ) = \(2^{2}\) = 4
1 | 1 4| 2 Теория: Чтобы найти НОД нескольких чисел, надо разложить
2 | 2 эти числа на простые множители ( как я и сделал ) и найти
1 | 1 произведение общих простых множителей, взяв каждый из них с наименьшим показателем. Одинаковые тут 2, берём с наименьшим показателем \( 2^{2}\) = 4
30 | 2 42 | 2 30= 2 * 3 * 5
15 | 3 21 | 3 42 = 2 * 3 * 7
5 | 5 7 | 7 НОД ( 30; 42 ) = 2 * 3 = 6
1 | 1 1 | 1
35 | 5 60 | 2 35 = 5 * 7
7 | 7 30 | 2 60= \(2^{2}\) * 3 * 5
1 | 1 15 | 3 НОД ( 35; 60 ) = 5
5 | 5
1 | 1

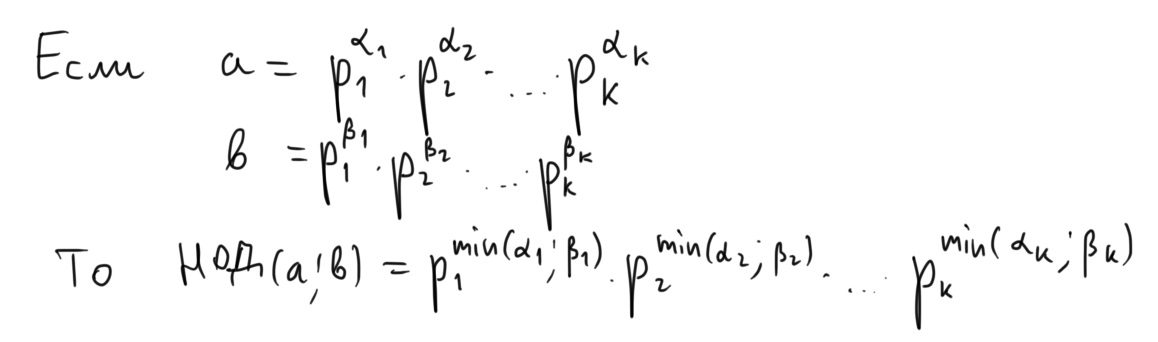
 Возьмём три числа: 60, 90 и 120. Каждое из них делится на 30. Значит число 30 есть делитель каждого из них. Принято говорить, что число 30 есть общий делитель чисел: 60, 90 и 120.
В дальнейшем нам часто придётся искать общий делитель для двух, трёх и т. д. чисел. Запомним, что общим делителем нескольких чисел называется число, на которое все данные...
Возьмём три числа: 60, 90 и 120. Каждое из них делится на 30. Значит число 30 есть делитель каждого из них. Принято говорить, что число 30 есть общий делитель чисел: 60, 90 и 120.
В дальнейшем нам часто придётся искать общий делитель для двух, трёх и т. д. чисел. Запомним, что общим делителем нескольких чисел называется число, на которое все данные...