График функции
- Графический способ решения уравнения mx = n
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... - Дробно-линейные функции
 Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех... - Линейные функции и их графики
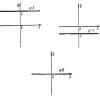 Рассмотрим равенство
у = 2х + 1. (1)
Каждому значению буквы х это равенство ставит в соответствие вполне определенное значение буквы у. Если, например, x = 0, то у = 2 • 0 + 1 = 1; если х = 10, то у = 2 • 10 + 1 = 21; при х = - 1/2 имеем у = 2 •...
Рассмотрим равенство
у = 2х + 1. (1)
Каждому значению буквы х это равенство ставит в соответствие вполне определенное значение буквы у. Если, например, x = 0, то у = 2 • 0 + 1 = 1; если х = 10, то у = 2 • 10 + 1 = 21; при х = - 1/2 имеем у = 2 •... - График квадратной функции
 Покажем, как строится график квадратной функции у = ax2 + bx + c. Наше рассмотрение придется разбить на ряд отдельных этапов.
1. График функции у = x2.
Этот график строится «по точкам». Составим следующую таблицу значений функции:
x
-3
-2
-1
-1/2
0
1/2
1
2
3
...
\(y=x^2\)
9
4
1
1/4
0
1/4
1
4
9
...
Отметим соответствующие точки на плоскости координат и соединим их плавной кривой (рис.). Эта кривая называется параболой.На рисунке парабола у = x2 начерчена лишь при -3...
Покажем, как строится график квадратной функции у = ax2 + bx + c. Наше рассмотрение придется разбить на ряд отдельных этапов.
1. График функции у = x2.
Этот график строится «по точкам». Составим следующую таблицу значений функции:
x
-3
-2
-1
-1/2
0
1/2
1
2
3
...
\(y=x^2\)
9
4
1
1/4
0
1/4
1
4
9
...
Отметим соответствующие точки на плоскости координат и соединим их плавной кривой (рис.). Эта кривая называется параболой.На рисунке парабола у = x2 начерчена лишь при -3... - Алгоритм исследования свойств квадратичной функцииОбласть определения. Область значений. Четность/нечетность функции. при b = 0 функция четная (то есть \(у = ах^2 +nс= а(-х)^2 + с\); при \(b \neq 0\), функция ни четная, ни нечетная. Нули функции. Если D > 0, то график квадратичной функции имеет два нуля: \(х_1 = \frac{-b -\sqrt{D}}{2a}; x_2 = \frac{-b +\sqrt{D}}{2a}\) и график функции пересекает ось х в 2-х точках. Если D = 0,...
- График логарифмической функции
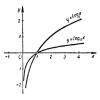 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение... - Свойства логарифмической функции
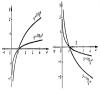 Рассмотрим основные свойства логарифмической функции
y = logax (1)
Напомним, что под а в формуле (1) мы подразумеваем любое фиксированное положительное число, отличное от 1.
Свойство 1. Областью определения логарифмической функции служит множество всех положительных чисел.
Действительно, пусть b есть произвольное положительное число. Покажем, что выражение \(\log_a b\) определено. Как мы знаем, \(\log_a b\) есть не что иное, как корень уравнения
аz = b (2)
Если...
Рассмотрим основные свойства логарифмической функции
y = logax (1)
Напомним, что под а в формуле (1) мы подразумеваем любое фиксированное положительное число, отличное от 1.
Свойство 1. Областью определения логарифмической функции служит множество всех положительных чисел.
Действительно, пусть b есть произвольное положительное число. Покажем, что выражение \(\log_a b\) определено. Как мы знаем, \(\log_a b\) есть не что иное, как корень уравнения
аz = b (2)
Если...
Примеры и задачи на график функции
- абсцисса точки пересечения графика функции
- график касательной к функции
- график линейной функции
- график степенной функции
- график убывающей функции
- график функции
- график функции заданной формулой
- график функции параллелен
- график функции пересекает
- дана функция y
- задайте эту функцию формулой
- изобразить схематически график функции
- исследовать на экстремум функцию
- найдите абсциссы точек пересечение графика
- найдите все значения, при которых график функции
- найдите координату точек пересечения графика функции
- найти координаты точки пересечения графиков
- найти точку пересечения графика функции осью
- найти угол наклона касательной к графику функции
- область определения функции
- построить график функции
- постройте график заданной функции найдите область
- постройте график функции у
- предел функции
- при каких значениях аргумента график функции
- при каких значениях параметра график функции
- принадлежат ли графику функции
- принадлежит ли графику функции
- промежутки возрастания и убывания функции
- проходит ли график функции
- точки пересечения графика функции
- укажите, через какие из данных точек проходит график
- уравнения касательной к графику функции
- функция задана формулой

 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех... Рассмотрим равенство
у = 2х + 1. (1)
Каждому значению буквы х это равенство ставит в соответствие вполне определенное значение буквы у. Если, например, x = 0, то у = 2 • 0 + 1 = 1; если х = 10, то у = 2 • 10 + 1 = 21; при х = - 1/2 имеем у = 2 •...
Рассмотрим равенство
у = 2х + 1. (1)
Каждому значению буквы х это равенство ставит в соответствие вполне определенное значение буквы у. Если, например, x = 0, то у = 2 • 0 + 1 = 1; если х = 10, то у = 2 • 10 + 1 = 21; при х = - 1/2 имеем у = 2 •... Покажем, как строится график квадратной функции у = ax2 + bx + c. Наше рассмотрение придется разбить на ряд отдельных этапов.
1. График функции у = x2.
Этот график строится «по точкам». Составим следующую таблицу значений функции:
x
-3
-2
-1
-1/2
0
1/2
1
2
3
...
\(y=x^2\)
9
4
1
1/4
0
1/4
1
4
9
...
Отметим соответствующие точки на плоскости координат и соединим их плавной кривой (рис.). Эта кривая называется параболой.На рисунке парабола у = x2 начерчена лишь при -3...
Покажем, как строится график квадратной функции у = ax2 + bx + c. Наше рассмотрение придется разбить на ряд отдельных этапов.
1. График функции у = x2.
Этот график строится «по точкам». Составим следующую таблицу значений функции:
x
-3
-2
-1
-1/2
0
1/2
1
2
3
...
\(y=x^2\)
9
4
1
1/4
0
1/4
1
4
9
...
Отметим соответствующие точки на плоскости координат и соединим их плавной кривой (рис.). Эта кривая называется параболой.На рисунке парабола у = x2 начерчена лишь при -3... Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение... Рассмотрим основные свойства логарифмической функции
y = logax (1)
Напомним, что под а в формуле (1) мы подразумеваем любое фиксированное положительное число, отличное от 1.
Свойство 1. Областью определения логарифмической функции служит множество всех положительных чисел.
Действительно, пусть b есть произвольное положительное число. Покажем, что выражение \(\log_a b\) определено. Как мы знаем, \(\log_a b\) есть не что иное, как корень уравнения
аz = b (2)
Если...
Рассмотрим основные свойства логарифмической функции
y = logax (1)
Напомним, что под а в формуле (1) мы подразумеваем любое фиксированное положительное число, отличное от 1.
Свойство 1. Областью определения логарифмической функции служит множество всех положительных чисел.
Действительно, пусть b есть произвольное положительное число. Покажем, что выражение \(\log_a b\) определено. Как мы знаем, \(\log_a b\) есть не что иное, как корень уравнения
аz = b (2)
Если...